So having watch this clip by Numberphile which explains why $0^0$ is undefined https://www.youtube.com/watch?v=BRRolKTlF6Q
And also this
And also this
Zero to the zero power – is $0^0=1$?
I understand how when given a function of the form $x^y$ then you have the following results
$$\lim_{x\rightarrow 0} x^0=1,$$ $$\lim_{y\rightarrow 0^+} 0^y=0,$$
and both the video and the mathforum link (and numerous others) mentioned about how when approaching form different directions you get different answers
However, both google and mathematica failed to actually show what the discontinuity look like
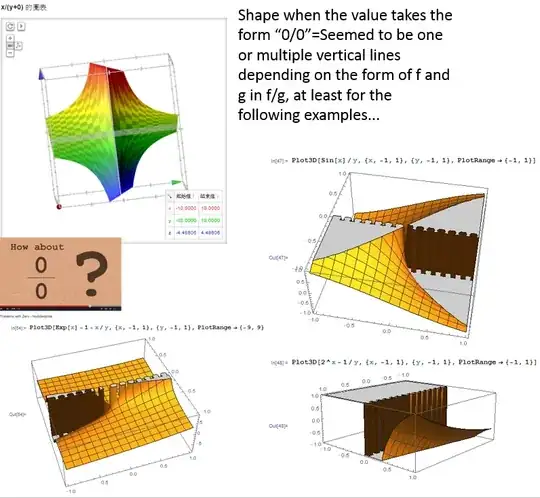
While a similar problematic case of "$\frac{0}{0}$" indeterminate form gives rather consistently the shape of the essential singularity
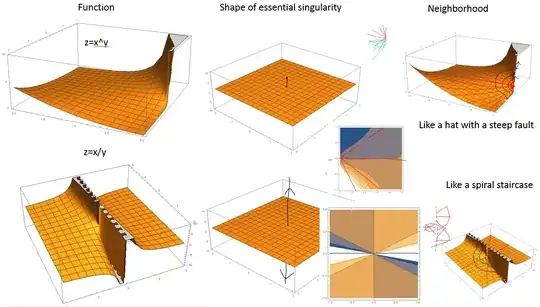
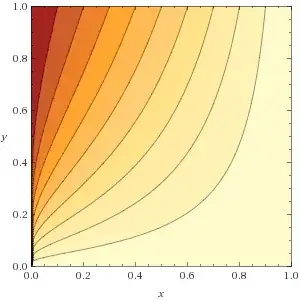
attempt to do so for the case $x^y$ in google and mathematica does not really illuminate the shape of the essential singularity
By approaching zero from the x axis, and also analysing the x and y partial derivatives of the function $x^y$ I can clearly see a jump
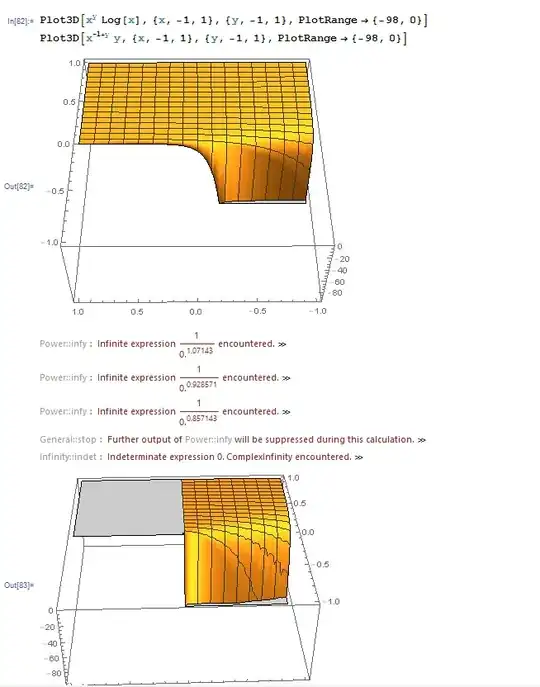
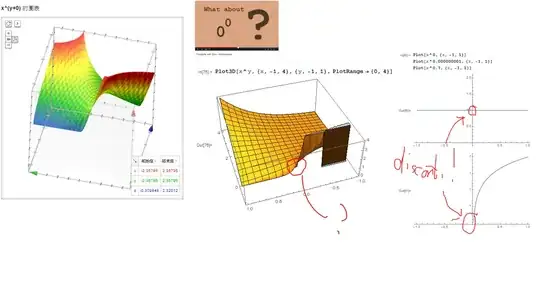
However I don't quite get what the result for the x^y cases as you approach from directions that are not x or y axis geometrically look like
For example, for the "$\frac{0}{0}$" case it is easy to see why Numberphile said the value of $\frac{0}{0}$ depends on the angle you approach the origin

But for $0^0$...
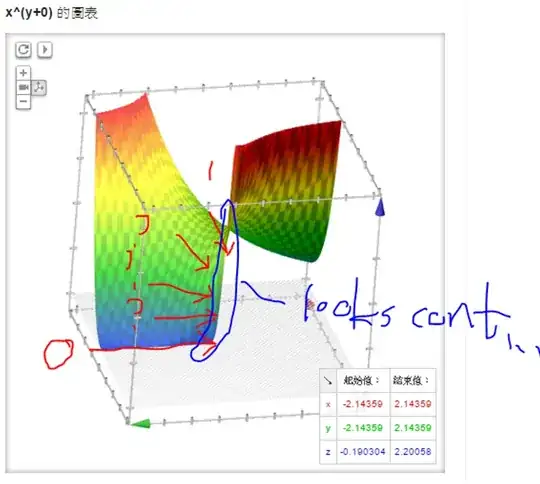
While algebraically the limits clearly evaluated to different values depending on how we approach it, geometrically it does not seeemed to agree with what the limits said (the curve look smooth and continuous...probably due to the limitation of the graphing programs)
"==============================================="
So to sum up my question,what does the discontinuity of $0^0$ actually look like, is it like an oscillation, a jump, a dot or something more complicated?
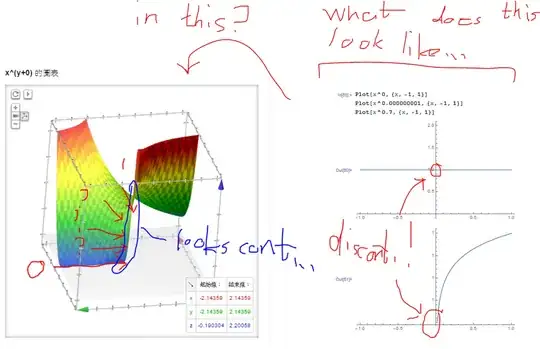
"==============================================="
UPDATE to ask for clarification, which should be in the comment section had it has a "posting image function")
Using the answers of Aes and Meelo, and examining the plots of the curves and parametric curves used by them to investigate the limiting behavior, I got the following
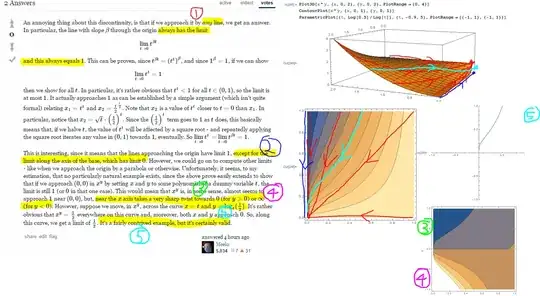
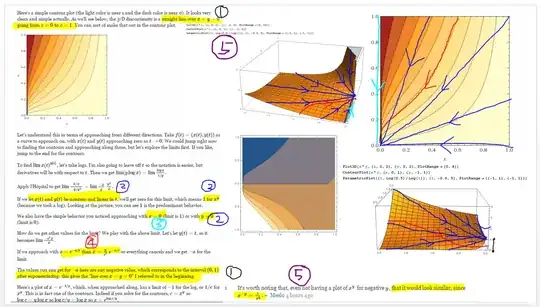
So the singularity has a shape of the vertical line interval (0,1) as mentioned by Aes and its neighborhood is as mentioned by Meelo has a very steep but non vertical "fault like structure"near the x axis which using the general form of a curve that can give limits that are between 0 and 1, as shown by Aes, explains why we need to travel along these curves (so that part of our journey is on that steep fault) in order not not get dragged into the value of 1
Or in short, based on the answers, is my understanding as shown below the correct way to understand it?