The way that differentials $dx, dy, $ etc are usually defined in elementary calculus is as follows:
Consider a $C_1$ function $f: \Bbb R \to \Bbb R$.
We define the tangent to the graph of $f(x)$ at the point $(c,f(c))$ to be $y=f'(c)(x-c) + f(c)$.
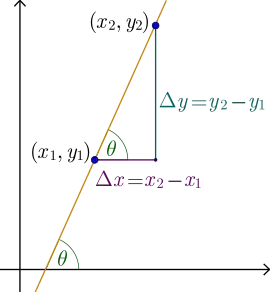
Here the value $x-c$ is called the increment of $x$, and is denoted $\Delta x$. So our tangent function can be written as $y=f'(c)\Delta x + f(c)$. Note that $\Delta x$ is actually evaluated at a specific value $c$ and thus should possibly be more correctly written as $\Delta x(c)$ or $\Delta x|_c$, but that'll get tedious so I'll leave off the explicit $c$ dependence.
Because the increment of $x$ can be just as easily defined on the graph of $f$ as on its tangent line $y$, we can also consider $\Delta x$ to be the differential of $x$, denoted $dx$. That is, we'll define $dx := \Delta x$. You can see that we could define all of the independent variables of a function in the same way for a function of multiple variables -- so for $g(x,y)$, we'd have $dx=\Delta x = x-c_1$ and $dy=\Delta y = y-c_2$.
The increment of the function $f$ is defined to be $\Delta f := f(c+\Delta x) - f(c)$. This is a measure of how much $f$ has changed given a change in $x$.
One of the fundamental ideas of calculus is that the increment $\Delta f$ should be approximately the same as the increment of its tangent $\Delta y$ for sufficiently small changes of $x$. From the above definition of the increment of a function, we can see that $\Delta y = y(c+\Delta x) - y(c) = [f'(c)((c+\Delta x) -c) + f(c)] - [f'(c)(c-c)+f(c)]$ $=f'(c)\Delta x + f(c) -0 -f(c) = f'(c)\Delta x$. Thus $\Delta y = f'(c)\Delta x$.
We define the differential of the function $f$ at $c$ to be equal to the increment of its tangent function. So $df|_c := \Delta y|_c$, or, dropping the $c$ dependence from our notation, $df:=\Delta y=f'(c)\Delta x$.
Notice that with these definitions, there is a fundamental difference between the differentials of independent variables -- like $dx$ -- and functions of those variables -- like $df$. Differentials of an independent variable is just the increment of that variable whereas the differential of a function is defined to be the increment of the tangent to that function, i.e. $df=\Delta y=f'(c)\Delta x=f'(c)dx$.
Also you should notice, that we define differentials (at least the differentials of functions) in terms of the derivative, not the other way around like early developers of calculus did. So we assume that a definition of the derivative has already been devised and agreed upon and we can then define our differentials in terms of that derivative.
NOTE: It is important that you realize that $\frac {df}{dx}$ is just a suggestive notation for $f'(x)$. It is NOT a fraction of differentials. In fact the only reason we use it is because it helps students learn things like the chain rule. But the derivative is actually defined by a limit, NOT by a ratio of infinitesimals (unless you're learning non-standard analysis).
So in response to your question: using the very first definitions given to students in elementary calculus. $df$ is literally defined by $df=f'(x)dx = \frac {df}{dx}dx$.
Now what are differentials used for? Differentials are an approximation of the change of a function for a very small change in the independent variable(/s). That is, $df \approx \Delta f$ when $\Delta x$ is sufficiently small.
In fact, the smaller that we make $\Delta x$, the smaller the difference between $df$ and $\Delta f$ becomes. The mathematical statement of this is that $\lim_{\Delta x \to 0} \frac {df}{\Delta f} = 1$. So $df$ and $\Delta f$ are "the same" for very, very small values of $\Delta x$.
Because OP seems to think that calculus is based on infinitesimals, I will try to elucidate this as fallacy. Notice that I did not use infinitesimals anywhere in this. $dx=x-c$ is finite. $df=f'(c)dx=f'(c)(x-c)$ is finite. There are no infinitesimals in this answer. And more generally in calculus, we don't use infinitesimals. Your first course in calculus you may have talked about them, but they are just meant to be a heuristic. No definitions actually require them.
One more thing to note: if you're familiar with Taylor's theorem, then let's look at the Taylor expansion of a $C_k$ function $f$ near the point $(c,f(c))$. We have $f(x) = f(c) + f'(c)(x-c) + \frac {f''(c)}{2!}(x-c)^2 + \cdots + \frac {f^{(k)}(c)}{k!}(x-c)^k + R$, where the remainder, $R$, is very small. Then you can see that the tangent function to the graph of $f$ is just the $1$st order Taylor expansion of $f$. And the differential $df$ is just the second term of Taylor expansion.
NOTE: IMO, a better, more useful definition of differentials is as differential forms. For a good reference, pick up the book Advanced Calculus: A Differential Forms Approach by Harold M. Edwards.