Since you want a physical interpretation of the differential elements, I'll assume you know what mechanical work is.
The differential elements are not really infinitesimals. That may have been how Newton and Leibniz thought about them, but in standard analysis today they are just linear functions.
Think about it this way. Say you have a constant force field -- for instance the gravitational force field near the surface of the Earth is constant to a very good approximation. Then consider a straight line segment -- positioned however you like -- in that force field. Now we'll say that that line segment is actually the path followed by a particle through the Earth's gravitational field -- so just pick one side of the line segment to call the starting position and the other end to be the final position of the particle.
Then the situation looks (in $2$d) like:
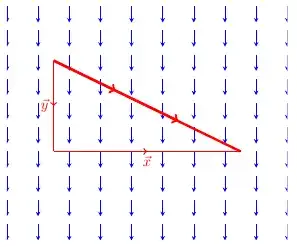
Now the differential form $F_x(x,y)dx + F_y(x,y)dy$ is just a function which assigns to oriented line segments, like the one above, a number. The $dx$ and $dy$ parts tell you by how much the $x$ and $y$ parts of the oriented line segment changes and the $F_x$ and $F_y$ are the $x$ and $y$ components of force at some point in each line segment. It also scales linearly with the length of those oriented line segments -- thus it is a linear function of line segements.
In this case, $dx$ is the function which associates the (signed) number $x$ to any oriented line segment $x\hat x + y\hat y$ and $dy$ is the function which associates the (signed) number $y$ to any oriented line segment $x\hat x+ y\hat y$, and we can choose any point along the path as our point at which to evaluate $F_x$ and $F_y$. Then the work due to gravity on this particle moving along the red path is $$W=F_x(x,y)dx + F_y(x,y)dy = mgy$$
Well, that was really easy, right. But what happens when $F_x$ and $F_y$ are NOT constant? Or when the path the particle follows is not a straight line -- but curved. In both cases we do the same thing: we approximate the answer by very small oriented lines segments. Then as we construct an approximation with smaller and smaller line segments our approximation should get better and better.
Here's a picture that might help you visualize what I mean. In it the black curve is the actual path and the blue and red curves are made of line segments to approximate the path. While the blue curve sort of approximates this sinewave, the red curve -- which has nearly $3$ times as many line segments -- follows the curve much more closely.
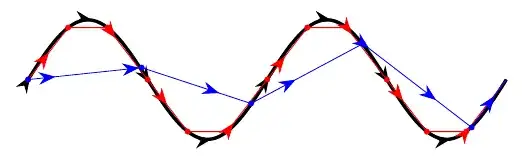
So for any partitioning we do of the curve, we end up with several oriented line segments at which to evaluate our differential form that we can then add to get an approximation for the work of the particle along the indicated path:
$$\text{Work} \approx \sum_i [F_x(x_i, y_i)dx_i + F_y(x_i, y_i)dy_i]$$
Then in the limit as the size of each line segment goes to zero (and assuming that everything is nice enough) we end up with the exact amount of work. So differential forms aren't infinitesimals -- they're just functions which associate line segments with numbers. Then integrals are defined as limits of sums of a differential form evaluated along many oriented line segments as the lengths of those line segments approach $0$.
Has that given you some intuition about what differential elements are?

