2

The classic proof for $\frac{\sin x}x\to1,x\to0$ is using a squeezing theorem based on arguments about areas of circles.

But as far as I know, all deduction of formula of circles' area is based on the fact $\frac{\sin x}x\to1,x\to0$. For example, using definition of definite calculus needs the fact to show limitation; using Newton-Leibniz formula needs to know $(\sin x)'=\cos x$, whose deduction also needs the fact $\frac{\sin x}x\to1,x\to0$.

So is it a circular reasoning?

AlexR
  • 24,905
Yiming Wang
  • 21

2 Answers2

3

If by "circular" you mean "related to circle" then there is a proof of $\lim\limits_{x \to 0}\dfrac{\sin x}{x} = 1$ which is circular.

If by "circular" you mean "a reasoning which uses its final result (to be established) as one of the intermediate steps to achieve the final result" then there is a proof of $\lim\limits_{x \to 0}\dfrac{\sin x}{x} = 1$ which is not circular.

I assume we are using the second meaning of "circular" here. The standard proof via using area of sector of circle to derive the inequalities $\sin x < x < \tan x$ is pretty well known and described by moderator robjohn in this answer.

There is no inconsistency in the above proof if we understand that this proof relies on the following facts:

1) A point $P$ on the unit circle $x^{2} + y^{2} = 1$ has the coordinates $(\cos \theta, \sin \theta)$ by definition where $\theta/2$ is the area of sector $AOP$ where $A = (1, 0), O = (0, 0)$. Note that the area of sector is also used to define measure of an angle and thus we say that the measure of $\angle AOP$ is $\theta$ (twice the area of sector $AOP$).

2) Area of triangle $AOP$ is less than area of sector $AOP$ which is further less than area of triangle $OAB$ where $AB$ is tangent to unit circle at $A$ and $OPB$ is a straight line.

3) The fundamental constant $\pi$ can be defined as total area of the unit circle which gives rise to $\sin (\pi/2) = 1, \cos (\pi / 2) = 0$.

These facts require the existence of area of sector of circle which is justified by the existence of the integral $\int_{0}^{x}\sqrt{1 - t^{2}}\,dt$ for all $x \in [0, 1]$. The additive properties of area can also be established if we use the definition of area as an integral and this justifies the inequalities between areas mentioned in 2) above.

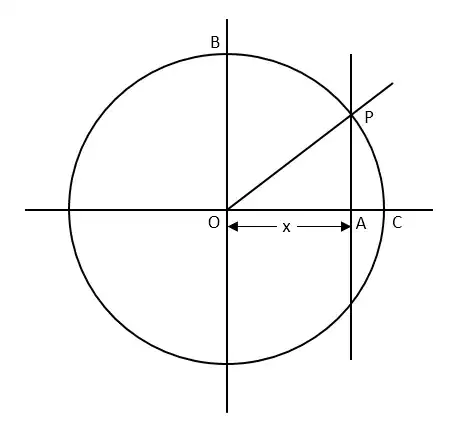
Note that the definitions of $\sin \theta, \cos \theta$ as mentioned in 1) are fully rigorous without any circular reasoning. Just to elaborate I will establish the formula $$\int_{0}^{x} \sqrt{1 - t^{2}}\,dt = \frac{x\sqrt{1 - x^{2}}}{2} + \frac{1}{2}\sin^{-1}x$$ directly from definitions of $\sin, \cos $ above. Area of OAPB

For this purpose set point $P$ on unit circle with coordinates $(x, \sqrt{1 - x^{2}})$. Let $O = (0, 0)$ be origin $A = (x, 0), B = (0, 1)$ and integral above represents area of $OAPB$ where $PB$ is the arc of circle. This area is clearly sum of areas of triangle $OAP$ and sector $OPB$. Clearly area of triangle $OAP$ is $$\frac{1}{2}\cdot OA \cdot AP = \frac{x\sqrt{1 - x^{2}}}{2}$$ Now we need to show that area of sector $OPB$ is $(\sin^{-1}x)/2$.

Let $C = (1, 0)$ and note that if $\angle POC = \theta$ then $$\sin \theta = AP = \sqrt{1 - x^{2}}$$ and then $$\begin{aligned}\angle BOP &= 2\cdot \text{area of sector }BOP\\ &= 2(\text{area of sector }BOC - \text{ area of sector }POC)\\ &= 2\cdot\frac{\text{area of unit circle}}{4} - 2\cdot\text{area of sector }POC\\ &= \frac{\pi}{2} - \angle POC = \frac{\pi}{2} - \theta\end{aligned}$$ Thus we get $$\sin \angle BOP = \sin\left(\frac{\pi}{2} - \theta\right) = \cos \theta = \sqrt{1 - \sin^{2}\theta} = x$$ It follows that $$\text{area of sector }BOP = \frac{1}{2}\angle BOP = \frac{1}{2}\sin^{-1}x$$

Community
  • 1
Paramanand Singh
  • 87,309
1

The Archimedes method:

enter image description here

Take it to be a n-sided polygon, ther area of such n-gon will be: $$A=n\left(\frac12bh\right)$$ Rearranging: $$A=\frac12(nb)h$$ where actually $nb$ is perimeter of the n-gon, so: $$A=\frac12Ph$$ when we increase n to a very large value, h just becomes the radius of a circle and from, the definition of $\pi$: $$\pi=\frac{P_{circle}}{diameter}=\frac P{2h}$$ So in that case: $$A\approx\frac12h(2\pi h)=\pi h^2$$

RE60K
  • 17,716
  • By the way the Archimedes method was not so simplistic. Rather his method was far more rigorous than what students can imagine in introductory calculus course. His reasoning was based on the fact that area of a circle is greater than area of inscribed polygon and less than area of a circumscribed polygon. Then Archimedes shows that when the number of sides of these polygons tends to $\infty$ then both the area of inscribed polygon and circumscribed polygon reach the same limiting value. Also he used a very different language which was perhaps easier to understand than limits. – Paramanand Singh Nov 01 '14 at 10:44
  • @ParamanandSingh that being uses upper and lower limits is right but i wanted to tshow that this is no circular reasoning, anyways thanks for your help – RE60K Nov 01 '14 at 18:06
  • In his proof, Archimedes needed to show that the perimeter of the circumscribed polygon was longer than the circle. He basically did this by assuming it to be true (i.e. he assumed that the boundary of a convex set was longer than the boundary of one of its convex subsets). – John Joy Nov 02 '14 at 16:31