3

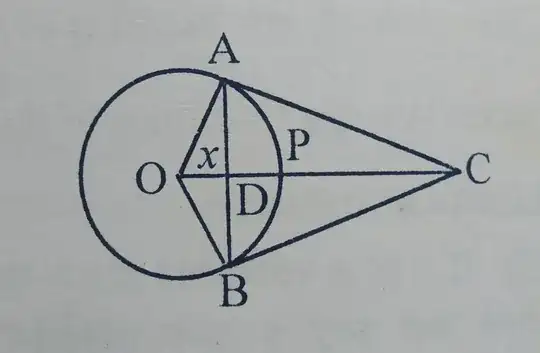
enter image description here

My book was proving $\lim_{x \to 0}\frac{\sin x}{x}$, and it dished out this line out of nowhere:

$$\text{chord}\ AB<\text{arc}\ APB<AC+BC$$

Now, I can get behind $\text{chord}\ AB<\text{arc}\ APB$. However, how does my book know that $\text{arc}\ APB<AC+BC$?

More info: The radius $OP$ bisects the chord $AB$

tryingtobeastoic
  • 3,176
  • 3
    hint: What is area of circular sector $OAPB$? How does it compare to area of kite $OACB$? – achille hui Oct 01 '21 at 11:50
  • @achillehui: How does the relation between the areas lead to a relation between the length of their boundaries? – Martin R Oct 04 '21 at 07:06
  • @MartinR for triangle, area = 1/2 base x height. for circular sector, area = 1/2 arc-length x radius. Since AC are tangent to the circle, the height of $\triangle OAC$ wrt AC is radius of circle. Same thing happens to $\triangle OBC$. – achille hui Oct 04 '21 at 07:18
  • @achillehui: What about posting that as an answer? – Martin R Oct 04 '21 at 07:44
  • @MartinR I was discussing the hint on CURED while debating why the below answer (which is now gone) is not appropriate. I'll probably post it. – Sarvesh Ravichandran Iyer Oct 04 '21 at 07:48
  • @MartinR my estimation is a semi-rigorous pure geometry based answer already take half a chapter to develop underlying concepts like what is "length" of a rectifiable curve, why the area of the sector is 1/2 arc-length x radius. etc. Failing to find an online source for this underlying material, this is way beyond what the answer in math.SE supposed to be. – achille hui Oct 04 '21 at 07:56
  • 2
    May I know a little more about the book you are reading @tryingtobeastoic? For context, see achille's comment above. The point is that the proof is expected to be along the following lines : the area of triangle $OAB$ is less than that of sector $OAPB$ which is less than that of the quadrilateral $OACB$, and the point is that the formulas for the area of the sector of the circle requires more rigorous discussion than is usually afforded for a mere discussion of $\frac{\sin x}{x}$. Thus I'd like to access your source and find out what is said about this particular formula. – Sarvesh Ravichandran Iyer Oct 04 '21 at 09:04
  • A similar question: https://math.stackexchange.com/q/2639679/42969. – Martin R Oct 04 '21 at 11:32
  • @TeresaLisbon I understand. Unfortunately, it is a local book and not that well known internationally, so I can't seem to find a link that I can give you. Thanks a lot for your concern! – tryingtobeastoic Oct 04 '21 at 11:58
  • 4
    @tryingtobeastoic We have a problem, unfortunately. You see, rigorously speaking, the biggest trouble with the argument is this : if I'm trying to find the area of a circle, then I approximate it by an $n$-gon, so I've got $n$ isosceles triangles with angles opposite base $2 \pi/n$ in each case. Thus, the area of this polygon is $n(r^2/2 \sin(2\pi/n))$ , and now you clearly see as $n \to \infty$, where I use the limit $\sin x / x$ itself! So it's confirmed that some circular stuff is going around. Now, there is one way in which this can be cleaned up, which is ... – Sarvesh Ravichandran Iyer Oct 04 '21 at 12:50
  • 3
    ... shown in this post. More precisely, over here, we can make sure that if $\pi$ is defined differently and if $\sin \theta, \cos \theta$ are defined using the area of the sector rather than, say as opposite over hypotenuse and so on, then the proof that $\frac{\sin x}{x} \to 1$ can be worked out, where one will have to switch the sin definition at some point of time. Basically, changing the definition of sin is a must. – Sarvesh Ravichandran Iyer Oct 04 '21 at 12:54

1 Answers1

1

However, how does my book know that $\;\text{arc}\ APB<AC+BC ?$

Noting that $OAC$ and $OBC$ are congruent triangles (due to the symmetry of $AC$ and $BC$ being tangents to the circle from a common external point), \begin{aligned} \text{arc } APB&=\frac2{OA}\times\text{area of sector } OAPB \\&< \frac2{OA}\times\text{area of kite } OACB\\&= \frac2{OA}\times OA\times AC\\&\text{(since the tangent $AC$ is perpendicular to the radius $OA$)}\\&=AC+BC.\quad\textit{(shown)} \end{aligned}

ryang
  • 38,879
  • 14
  • 81
  • 179