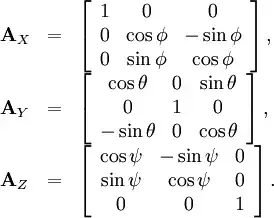Summary taken from my original question and answer here..
First of all as Nicol suggested you are mixing up the reality with how computers or the mechanics of the gimbals work. You are taking an analogy literally.
If we scratch the whole concept of gimbals and see how rotations work in terms of maths, the idea is quite simple. The rotations around the 3 axes are described by the matrices..
Note however, that these matrices don't know the difference between global and local axes. By global, I mean axes that remain fixed in space no matter the rotations applied and the local are axes/frame fixed with the body so it moves accordingly. So when it comes down to math the rotation matrix is going to change the values in the same way it was doing the first time. So for e.g if we apply a $A_{x}({90^{\circ}})$ to a standard frame like in your first picture, it'd move the $Y$ axis to $Z$ and $Z$ to $-Y$ assuming counter-clockwise rotation for right handed system. Now if you apply a $A_{y}({u^{\circ}})$ with a random angle, the matrix is still gonna rotate around the previous $Y$ which is currently the local $-Z$ not the new local $Y$ axis.
This is because matrix multiplication only modifies the respective columns/rows. If Y-axis was in the middle column at the beginning and then after a rotation the middle column values changed to Z-axis $(0,0,1)$ that doesn't mean it's going to rotate around the Z-axis next. Graphically speaking the rotation is still around the global Y-axis no matter what the values of the middle column are. If you have trouble understanding this try doing what I explained on a piece of paper and you'll see what I mean.
Moving on, once you understand that, the second concept to understand is that euler angles work with chained rotations. So stuff like $x-y-z$ or $z-y-z$. The key thing to note is that the concept of gimbal lock appears after you apply 1 or 2 of those rotations in order within a specific chained rotation, say $x-y-z$. This is important because if you forget this you are gonna ask the question "Well, why can't we just move the other axes?" You can't because you are following a specific order of three chained rotations and you have already done the first one or two rotations.
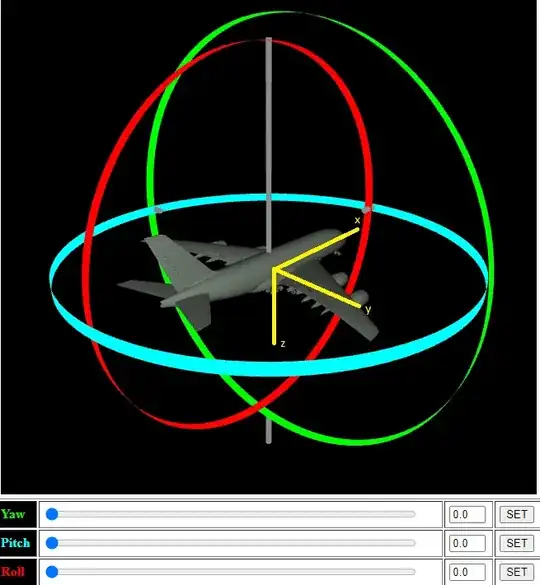
That being said, now you can imagine an aeroplane with the orientation

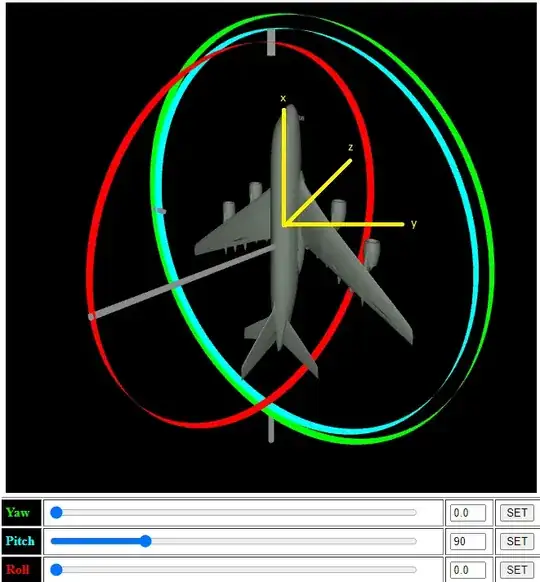
Note here, that if you rotate around the $X$ you'll either roll left/right. Assume we are following the order $x-y-z$. Next assume we rotated around the $X$ axis a little so we can see the plane's bottom and then rotated $90$ degrees around the $Y$. This is how it'd look like

Now here's the gimbal lock. If you try to rotate around the $Z$ axis it's the same rotation back when you were rotating around the $X$. That is, the plane is only rolling. We lost 1 degree of freedom.
You might be thinking well but now, rotation around the $X$ rotates differently so we haven't lost any freedom at all. True but that's thinking again outside the concept of the chained rotation order. We have already done rotation around $X$ and $Y$ so the order only leaves us $Z$ but due to a certain angle of rotation around the $Y$ we can't uniquely rotate it in the third dimension. That's the gimbal lock. If you break free from the order, then it's really hard to perceive the idea of the loss of the degree of freedom.
In applied mathematics terms, this is what's happening...
We have our rotation order $x-y-z$ with the corresponding angles $\alpha-\beta-\gamma$,
$$
R =
\begin{bmatrix}
\cos \gamma & -\sin \gamma & 0 \\
\sin \gamma & \cos \gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos \beta & 0 & \sin \beta \\
0 & 1 & 0 \\
-\sin \beta & 0 & \cos \beta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \alpha & -\sin \alpha \\
0 & \sin \alpha & \cos \alpha
\end{bmatrix}
$$
Now just to explain what's really going on we skip applying the first rotation and directly rotate 90 degrees around $Y$ which would be $\beta = 90$
$$
R =
\begin{bmatrix}
\cos \gamma & -\sin \gamma & 0 \\
\sin \gamma & \cos \gamma & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 1 \\
0 & 1 & 0 \\
-1 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \alpha & -\sin \alpha \\
0 & \sin \alpha & \cos \alpha
\end{bmatrix}
$$
$$
R =
\begin{bmatrix}
\cos \gamma & -\sin \gamma & 0 \\
\sin \gamma & \cos \gamma & 0 \\
0 & 0 & 1 \end{bmatrix}
\begin{bmatrix}
0 & \sin \alpha & \cos \alpha \\
0 & \cos \alpha & -\sin \alpha \\
-1 & 0 & 0 \end{bmatrix}
$$
Now multiplying these, we get,
$$
R =
\begin{bmatrix}
0 & \cos\gamma * \sin\alpha -\sin \gamma * \cos\alpha & \cos\gamma * \cos\alpha + \sin \gamma * \sin \alpha \\
0 & \cos\gamma * \cos\alpha + \sin \gamma * \sin \alpha & -\cos\gamma * \sin\alpha +\sin \gamma * \cos\alpha \\
-1 & 0 & 0 \end{bmatrix}
$$
$$
R =
\begin{bmatrix}
0 & \sin(\alpha - \gamma) & \cos(\alpha - \gamma) \\
0 & \cos(\alpha - \gamma) & -\sin(\alpha - \gamma) \\
-1 & 0 & 0 \end{bmatrix}
$$
As you can see, changing either $\alpha$ or $\gamma$ here gives us the same matrix. Which means rotation around the $X$ or the $Z$ axis gives us the same result resulting in a loss of 1 degree of freedom.
Personally speaking all those images of gimbals always confused the hell out of me. For a graphics guy it'd have been much more clearer if people explained it more in terms of applied mathematics i.e. Matrices and such and used the diagrams of perpendicular axes instead of gimbals.
What the artiles explaining this concept in terms of gimbals don't do is map the gimbal analogy to the axes analogy. In gimbals there is the concept of parenting. So moving the innermost or I guess the red gimbal in your case won't move the outer two. Moving the outermost will move the other two. This feels really confusing if you have the global/local axes analogy in mind and you are thinking of the gimbals as axes since here both local/global seem all mixed. The idea of the gimbals and parenting here is to preserve the way the previous rotation rotates the object so that when the gimbals align you can actually see that the previous and the new rotation rotate in the same way. So if we have the order $x-y-z$ The innermost gimbal would correspond to $x$. Think of the gimbals appearing one by one after each rotation is applied and not being there from the start.
So considering my example of the plane, rotation around the $x$ does the rolling. The gimbal tied to it is the innermost. So that when you apply rotations around $y$ and $z$ the $x$ gimbal would move with them in order to preserve the rolling aspect.