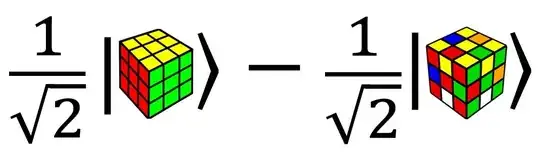Introduction
Consider a state $\vert\psi\rangle$ such as below, which is in a superposition of a difference between a Rubik's cube in a solved state and a Rubik's cube in the "superflip" state.
Here, with eight cells on each face (apart from the fixed center cell), six faces, and three qubits (or one qubit and one qutrit) to record the color of each cell, $\vert\psi\rangle$ can be encoded with $8\times 6\times 3=144$ qubits.
A circuit to simulate the cube
We can describe the Rubik's Cube Group as the group generated by various twists of the faces of the cube, where each twist is a simple quantum circuit acting on these qubits, and use this to construct a Hamiltonian that simulates a (classical) random walk along the Laplacian matrix for the Cayley graph of the cube. For example, letting:
$$\langle F_1,B_1,L_1,R_1,U_1,D_1,F_2,B_2,L_2,R_2,U_2,D_2,F_3,B_3,L_3,R_3,U_3,D_3\rangle$$
be a generating set of $\mathsf{SWAP}$ circuits for the quarter-turn, half-turn, and three-quarter turn twists of each of the front, back, left, right, up, and down face, and choosing a Trotter factor of four, we can simulate $\mathcal H_{\text{Rubik's}}$ as:
$$e^{-i\mathcal H_{\text{Rubik's}}}\approx\big(\sqrt[4]{F_1}\sqrt[4]{B_1}\sqrt[4]{L_1}\sqrt[4]{R_1}\sqrt[4]{U_1}\sqrt[4]{D_1}\sqrt[4]{F_2}\cdots \sqrt[4]{D_2}\sqrt[4]{F_3}\cdots\sqrt[4]{D_3}\big)^4=:W;$$
that is, $W$ is a circuit that iterates each of the fourth roots of each of the generators four times.
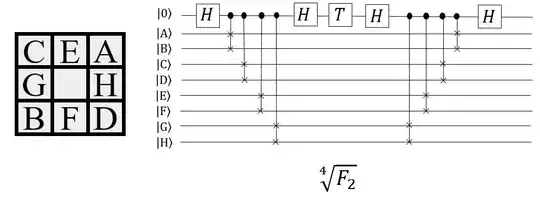
Some other ideas help to clarify how to take such roots for each such generator. For example, the half-turn moves $F_2,B_2$, etc. all have order two (e.g. $F_2^2=F_2 F_2=\mathbb 1$), and we can use a single ancilla to corresponding to the respective $\pm 1$ eigenspace. An example of $\sqrt[4]{F_2}$ is illustrated below, with the ancilla at the top (I'm only showing eight cells for brevity).
Each of $\vert \mathrm{A}\rangle,\vert \mathrm{B}\rangle,$ etc. are three-qubit registers (or as mentioned, one-qutrit, one-qubit registers) that can be in a superposition of the six possible colors.
The circuits for the roots for the quarter-turn generators $F_1,F_3$, etc. are only slightly more complicated, as there the order is four (e.g. $F_1^4=F_3^4=\mathbb 1$ with eigenvalues $\pm1, \pm i$), and they would require two ancillae instead of just the one.
Quantum phase estimation of the cube
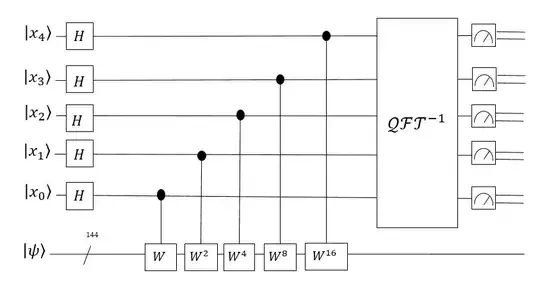
Nonetheless we have a natural probability distribution for a Hamiltonian $\mathcal H_\text{Rubik's}$ acting on $\vert\psi\rangle$ with support being the $\mathcal H_{\text{Rubik's}}$ eigendecomposition of $\vert\psi\rangle$. Indeed, with a quantum phase estimation circuit as below, we can sample from such a distribution, with $5$ qubits of precision.
If we were able to execute and sample such a circuit acting on various superpositions of the cube, could we learn anything about how difficult it is to walk from various states to each other?
For example, my intuition is that if $\vert\psi\rangle$ is in a superposition $\frac{1}{\sqrt 2}|J\rangle-\frac{1}{\sqrt 2}|K\rangle$ of the Rubik's cube with $J$ and $K$ being two configurations of the cube that are close to each other under the appropriate word metric, then most of the eigenvalues sampled will be close to zero, whereas the superposition of the solved state minus the superflip state likely has a decomposition with most eigenvalues far away from zero.
This is based on some ideas from Janzing and Wocjan (1, 2, 3) on some (promise) BQP-complete problems with large matrices. Also, I use five qubits with $W$ being applied up to thirty-one times, because that's more than the twenty twists associated with the diameter of the cube, and hence I intuit that thirty-one steps would be classically infeasible, but it might still be interesting and classically challenging even if a controlled-$W$ were applied only once. Lastly I take it for granted that we can prepare a state such as $\vert\psi\rangle$ by optimizing a clever sequence of Hadamards and CNOT's/CZ's with a mapping of qubits to colors; this state-preparation question was noted and assumed straightforward in Janzing and Wocjan (and also HHL).