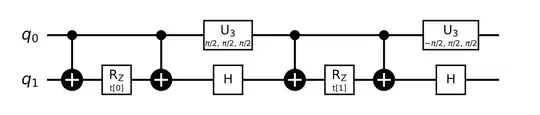
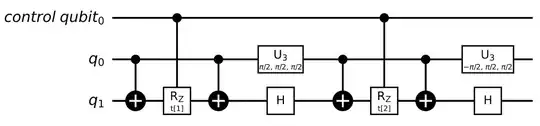
I had a question last week regarding the simulation of Hamiltonians composed of the sum of Pauli products: How can I simulate Hamiltonians composed of Pauli matrices? I'm having a follow-up question: still for those two Hamiltonians: $$ H_{1} = X_1+ Y_2 + Z_1\otimes Z_2 \\ H_{2} = X_1\otimes Y_2 + Z_1\otimes Z_2 $$ How can I perform the 'controlled version' of them? The thing really confused me is the 'tensor product term': for both $H_1$ and $H_2$, the two qubits are coupled, but if I want to do the controlled time-evolution simulation, should I couple the whole thing with the third qubit? If so, how to do that?
Thanks:)