I'm reading a Hamiltonian simulation example proposed in this paper. From their notation, the operator $D_y$ (sometimes it's called $H_y$) serves the function to diagonalize the Pauli matrix $\sigma_y(Y)$ (the corresponding circuit is illustrated below):
$$
D_y\ (or\ H_y)=HSX=\frac{1}{\sqrt{2}}\begin{bmatrix}
i & 1\\
-i & 1
\end{bmatrix}
\quad\quad\quad [A]
$$
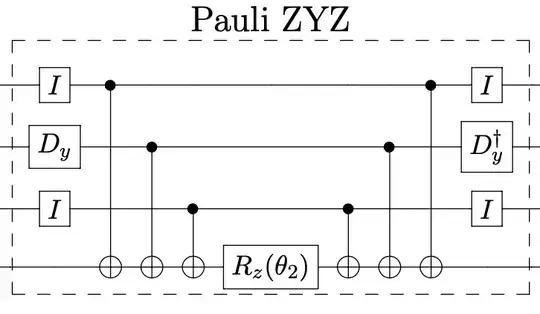
However, unlike $D_x$, which is the Hadamard gate, I found $D_y$ is sometimes written in different ways, like in this answer by @Craig Gidney:
$$ D_y\ (or\ H_{YZ}) = \frac{Y+Z}{\sqrt{2}} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & -i\\ i & -1 \end{bmatrix} \quad\quad\quad [B] $$
and in this answer by @Davit Khachatryan:
$$ D_y\ (or \ 'Y'_{not\ pauli\ here}) = U_2(0,\pi/2) =\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & -i\\ 1 & i \end{bmatrix} \quad\quad\quad [C] $$
Thus I'm wondering are those different versions of $D_y$ the same thing? Are they essentially all belong to $U_2$ gate?
Also, when should we use two $U_3$ gates outside of the CNOT gates to perform the time-evolution simulation (like in this case, the answer from @KAJ226)?
Thanks!!!