8

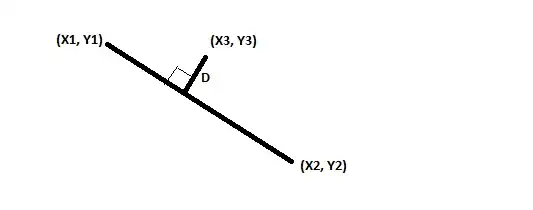
I am a computer programmer and need to find the x and y coordinate of a point that is a defined perpendicular distance from a midpoint. For reference, I have tried to attached an image for reference.

X1, Y1, D, X2, Y2 will be given. I need to find X3, Y3. The shorter line, will always be perpendicular from the larger line and will always intersect the midpoint between (x1, x2) and (x2, y2). I have been struggling with this a while and cannot figure it out. Any help would be greatly appreciated.

for reference

brick
  • 1,919
tpdietz
  • 183

4 Answers4

8

The midpoint is the average of the two endpoints: $$ (\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}). $$ If I understand correctly, you want to move from this midpoint a distance $D$ in a direction perpendicular to the line joining points 1 and 2. The direction from 2 to 1 is given by the vector $$ (x_1-x_2,y_1-y_2). $$ A vector perpendicular to this one is $$ (y_1-y_2,x_2-x_1). $$ We want a vector of this (or the opposite) direction and length $D$ attached to the midpoint, so the final point will be $$ (x_3,y_3) = (\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}) \pm \frac{D}{\sqrt{(y_1-y_2)^2+(x_2-x_1)^2}}(y_1-y_2,x_2-x_1). $$

Joonas Ilmavirta
  • 25,809
3

Given $(x_1, y_1), (x_2, y_2)$ the midpoint $P$ is

$$P = (X, Y) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right).$$

The slope of the perpendicular is the negative reciprocal of the slope of the line segment:

$$m = -\frac{x_2 - x_1}{y_2 - y_1}.$$

Then, the line going through the midpoint perpendicular to your line segment is defined by

$$y - Y = m(x - X),$$

which allows you to solve for $y$ in terms of $x$ for all points on the perpendicular.

Finally, find the values of $x_3,y_3$ such that

$$(X-x_3)^2 + (Y-y_3)^2 = d^2.$$

You should get two choices (or one, if $d=0$ -- in that case, it's just $P$!)

John
  • 26,319
2

You can easily find the midpoint $M = \frac{1}{2}(x_1, y_1) + \frac{1}{2}(x_2, y_2)$. The perpendicular vector is $(-y_2 + y_1, x_2 - x_1)$. The only thing left is to make it $D$ long and add it to $M$.

brick
  • 1,919
1

The formula for the midpoint is

$$ \left(\frac{X_1 + X_2}{2}, \frac{Y_1 + Y_2}{2}\right) $$

To find the distance between two points

$$ \sqrt{(X_1 - X_2)^2 + (Y_1 - Y_2)^2} $$

Jack
  • 764