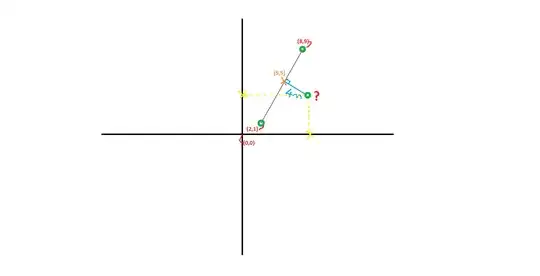
You may find this too elementary, but 3rd grade arithmetic is what I do.
While your points will work just fine in the method I want to show you, they are not good for demonstration because the change in x and the change in y are both equal to 6, which adds unneeded confusion.
Let's use points. $A=(2,3)$ and $B=(5,7)$. Begin by defining a midpoint,P. $$P=\left(\frac{A_x+B_x)}{2},\frac{A_y+B_y}{2}\right)=\left(\frac{2+5}{2},\frac{3+7}{2}\right)=\left(3.5,5\right)$$ Next, we will define the change in x and change in y. $$\Delta x=B_x-A_x=5-2=3$$ $$\Delta y = B_y-A_y=7-3=4$$ We need to keep up with the sign of these numbers and always do the subtractions in the correct order. Now I am going to define a new number, n, which will be the distance in kilometers (whatever units) between the two points. $$n=\sqrt{\Delta x^2+\Delta y^2}=\sqrt{3^2+4^2}=\sqrt{25}=5$$
Now I will define a vector. This isn't difficult, so stay with me. These will be just numbers. $$v_{\perp}=\left(\begin{array}{c}
\frac{-\Delta y}{n}\\
\frac{\Delta x}{n}
\end{array}\right)=\left(\begin{array}{c}
\frac{-4}{5}\\
\frac{3}{5}
\end{array}\right)=\left(\begin{array}{c}
-0.8\\
0.6
\end{array}\right)$$ Incredibly, this vector tells us which direction to go away from the line and it will always be perpendicular to the line (either up or down, left or right).
Finally, we are going to calculate the new postion, which we want to be 4 kilometers from the middle and at a right angle from the line between A and B. The $"\pm"$ in the equation below is because I don't know whether you are going left or right from the midpoint. Let $$d=4$$
$$\text{New Position }=P \pm d\cdot v_{\perp}$$ To show you how to do this calculation, I will write midpoint P as a vector.$$\text{midpoint}=P=\left(\begin{array}{c}
3.5\\
5
\end{array}\right)$$
$$\text{New Position }=P \pm d\cdot v_{\perp}=\left(\begin{array}{c}
3.5\\
5
\end{array}\right)\pm 4\cdot \left(\begin{array}{c} -0.8\\0.6\end{array}\right) $$
Doing the Plus part, $$\text{New Position }=\left(\begin{array}{c}3.5+4(-0.8)\\5+4(0.6)\end{array}\right)=\left(\begin{array}{c}3.5-3.2\\5+2.4\end{array}\right)=\left(\begin{array}{c}0.3\\7.4\end{array}\right)=(0.3,7.4)$$
Doing the Minus part, $$\text{New Position }=\left(\begin{array}{c}3.5-4(-0.8)\\5-4(0.6)\end{array}\right)=\left(\begin{array}{c}6.7\\2.6\end{array}\right)=(6.7,2.6)$$