0

I know there is a similar question to this one. However, the method used there is slightly different; I would like to know what is wrong with my method

I tried to prove that the surface area of a cone is $\pi rs$, where s, is the slant height of the cone. This can be proved by "opening up" the cone and using the sector of a circle obtained.

This is the method I used:

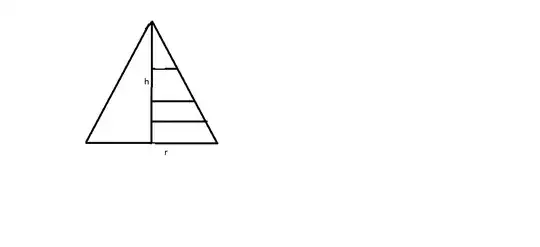
enter image description here

$h$ is the height of the cone, and $r$ is the radius of the base

Shouldn't $\int_{0}^{h} {2\pi rx \over h} \delta x$ equal the curved surface area, as $ r x\over h$ will represent the radius of each disc obtained, when cut along the base of the cone, for each height from 0 to h.

However, simplifying the expression leaves me with $\pi rh$ and not $\pi rs$. Why is my method wrong?

Community
  • 1
Tejas Ramdas
  • 119

1 Answers1

0

I think the difference is due to the approximation for the surface area:

$dS=\frac{2\pi rx}{h}\delta x$

not been accurate, the area is related to the longitude of $\delta s$ (see figure) : enter image description here

The correct value for surface area will be:

$dS=\frac{2\pi rx}{h}\delta s$

The difference in the two measures can be seen more clearly if you exaggerate the angle of the cone, as I tried to do in the figure. So if you still want to calculate the area by means on an integral from 0 to h (the range of values that x can take), this is: $\int_0^h\frac{2\pi rx}{h}\delta s$

You will need to express $\delta s$ in terms of $\delta x$

$\delta s=\delta x \frac{s}{h}$

Which will correct your previous result to the correct value. Otherwise you can try to express $dS$ only in terms of the s variable and perform the integration over the range of values that s can take, this is from 0 to S.

The bottom line is, not every "infinitesimal" approximation is necessarily correct.

Francisco Angel
  • 23