How do I prove $\lim_{\theta \to 0}{\frac{\sin \theta}{\theta}}=1$ when $\theta$ is positive using $\frac{1}{2}r^2(\theta-\sin \theta)$? The last formula gives the area of the shaded area in the image below:
I have proved that $\lim_{\theta \to 0}{\frac{\sin \theta}{\theta}}=1$, but using a different method. The book I am working in asks to use the formula above to prove the limit geometrically. I have tried for some time, but don't seem to get anywhere. Any ideas?
We will only deal with positive $\theta$, but then negative $\theta$ are no problem, since $\sin(-\theta)=-\sin\theta$, and therefore $\frac{\sin(-\theta)}{-\theta}=\frac{\sin \theta}{\theta}$.
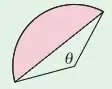
Let $r=1$. Look at the area of the "ice-cream" (shaded part). The intuition is that if $\theta$ is small, then this area is negligible compared to the area $\theta/2$ of the full sector. But this has to be shown.
If $\theta$ is close to $0$, the shaded region has area that is less than the area of a half-circle with diameter the given chord. The half-chord has length $\sin(\theta/2)$. We conclude that $$0<(1/2)(\theta-\sin\theta)<(1/2)\pi\sin^2(\theta/2).$$ Multiply by $2$, divide by $\theta$. We get $$1-\frac{\sin \theta}{\theta}<\frac{\pi\sin^2(\theta/2)}{\theta}.$$ But since $\sin\theta<\theta$, and $\sin(\theta/2)<\sin\theta$, we have $$\frac{\pi\sin^2(\theta/2)}{\theta}<\pi\sin(\theta/2).$$ Now let $\theta\to 0^+$. Then $\pi \sin(\theta/2) \to 0$, so by "squeezing" $$\lim_{\theta\to 0^+} 1-\frac{\sin \theta}{\theta}=0.$$
Comment: There are other ways perhaps better ways to find a small enough upper bound for the area of the shaded region. For example, extend the arms of the sector so they have length $\sec(\theta/2)$ and join the ends of the arms. We get a triangle with area $(1/2)\tan(\theta/2)$. So the shaded region has area less than $$(1/2)\tan(\theta/2)-\sin(\theta/2), $$ which simplifies to $(1/2)\sin(\theta/2)(\sec(\theta/2)-1)$. This gives us the bounds $$0<\theta-\sin\theta<\sin(\theta/2)(\sec(\theta/2)-1).$$ As before, divide both sides by $\theta$. Since $\sin(\theta/2)/\theta<1$, and $\sec(\theta/2)-1$ approaches $0$ as $\theta$ approaches $0$, again squeezing gives the desired result. The machinery used in this comment is closely related to the "standard" geometric argument for the limit of $\frac{\sin \theta}{\theta}$.
Actually, you do not really have to use $\frac{1}{2}r^2(\theta-\sin \theta)$. Check out this/these website[s] for more information:
