1

Possible Duplicate:
Proving $\lim_{\theta \to 0}{\frac{\sin \theta}{\theta}}=1$ using $\frac{1}{2}r^2(\theta-\sin \theta)$

How can one prove that $$\lim_{\theta \to 0} \frac{\sin\theta}{\theta}=1$$

$\sin(0) = 0$

Community
  • 1
HOLYBIBLETHE
  • 2,770
  • It is best to leave the duplicated link in the body of the text, so that one can actually view the duplicated result! – JavaMan Aug 31 '12 at 07:12

2 Answers2

1

$\lim_{\theta \rightarrow 0} \frac{\sin(\theta)}{\theta} = \lim_{\theta \rightarrow 0} \cos(\theta) = 1$ by L'hopital's rule.

Euler....IS_ALIVE
  • 4,707
1

For sufficiently small positive values of $\theta$:

$$\sin \theta \leq \theta \leq \tan\theta$$

This can be shown geometrically (picture is from here):

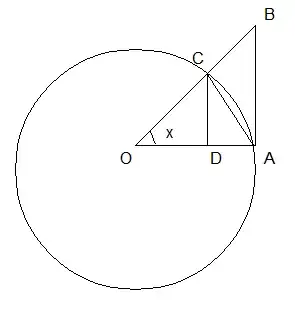
enter image description here

The area of $\Delta OAC$ is $\frac 12 \cdot 1 \cdot \sin x=\frac 12\sin x$. The area of the circular sector $AOC$ is $\frac x2$. The area of triangle $\Delta OAB$ is $\frac12\cdot 1\cdot \tan x=\frac 12\tan x$. Noting that these shapes are contained within each other (and rewriting the variable $x$ as $\theta$ for consistency), we write

$$\frac 12\sin \theta\leq\frac \theta2\leq\frac 12\tan \theta$$ $$1\leq\frac{\theta}{\sin\theta}\leq\frac 1 {\cos\theta}$$ $$\cos\theta\leq\frac{\sin\theta}{\theta}\leq1$$

Take $\lim_{\theta\to 0^+}\cos\theta$ and apply the squeeze theorem. Just flip the inequalities around in the first line for the negative case. When you go to the second line by dividing by $\sin\theta$, which is negative then $\theta$ is negative, the rest of the argument proceeds the exact same way.

Robert Mastragostino
  • 15,727
  • How does one show that $\sin(\theta)\le\theta\le\tan(\theta)$? – robjohn Mar 27 '13 at 17:44
  • There's a great treatment of a geometric proof by areas here. Should I update my answer with more information? – Robert Mastragostino Mar 28 '13 at 12:03
  • That looks very similar to my answer. Since this is a key inequality, something more might be said. – robjohn Mar 28 '13 at 14:55
  • how does one show that the area of a circle is $\pi r^2$ without assuming that $\lim\limits_{x\to 0}\frac{\sin x}{x} = 1$? see http://math.stackexchange.com/questions/605915/find-the-limit-displaystyle-lim-x-to-0-sin-x-frac1-ln-x/775759#775759 for a similar answer. – John Joy Jul 01 '14 at 15:23
  • @JohnJoy what's your definition of $\pi$ to start with? There are plenty that don't need to make any reference to trig functions whatsoever. They might assume facts that end up being logically equivalent to $\lim_{x\to 0} \sin x/x=1$, but I don't see how it's inevitably circular. – Robert Mastragostino Jul 01 '14 at 22:09
  • If they assume facts that are logically equivalent, then you can't use one to prove the other without descending into circular logic. My biggest issue with such proofs has always been $x\lt\tan x$ (which is equivalent to $\cos x\lt\frac{\sin x}{x}$). But upon further consideration, I realize that you could prove this fact by assuming that the boundary of a convex set is larger than the boundary of one of its convex subsets. – John Joy Jul 02 '14 at 01:11