Find $\lim_{n\to\infty}\sqrt{6}^{\ n}\underbrace{\sqrt{3-\sqrt{6+\sqrt{6+\dotsb+\sqrt{6}}}}}_{n\text{ square root signs}}$

Question

We have the following representation of pi: $$\pi=\lim_{n\to\infty}2^n \underbrace{\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\dotsb+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}}}}}}_{n\text{ square root signs}}$$ which can be proven using the identity $\sin\left(\dfrac\pi{2^{n+1}}\right)=\dfrac12\underbrace{\sqrt{2-\sqrt{2+\sqrt{2+\dotsb+\sqrt{2}}}}}_{n\text{ square root signs}}$. (There's similar one for $\cos$, except without the minus sign.)

---

This made me wonder: Is there a closed form for: $$\lim_{n\to\infty}3^n \underbrace{\sqrt{3-\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6+\dotsb+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6}}}}}}}}}}_{n\text{ square root signs}}$$ (Note that $\sqrt{6+\sqrt{6+\sqrt{\dots}}}=3$, so this question is of the form $\infty\times0$.)

EDIT: It seems like that doesn't converge, but this does: $$\lim_{n\to\infty}\sqrt{6}^{\ n}\underbrace{\sqrt{3-\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6+\dotsb+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6}}}}}}}}}}_{n\text{ square root signs}}\approx4.49377$$

Answer 1

I did not find a closed form, but I show existence of the limit, and find a very good correction for the error at a finite termination.

---

Convergence

Define $a_0=0$ and $$ a_{n+1}=\sqrt{6+a_n}\tag{1} $$ Then $$ \begin{align} \frac{3-a_{n+1}}{3-a_n} &=\frac{3-\sqrt{6+a_n}}{3-a_n}\\ &=\frac1{3+\sqrt{6+a_n}}\\ &\le\frac1{3+\sqrt6}\tag{2} \end{align} $$ Note that $(2)$ implies that $a_n$ increases monotonically from $0$ to $3$.

Inductively, we get $$ |\,3-a_n\,|\le\frac3{(3+\sqrt6)^n}\tag{3} $$ Therefore, $$ \begin{align} \frac{6^{n+2}}{6^{n+1}}\frac{3-a_{n+1}}{3-a_n} &=\frac6{3+\sqrt{6+a_n}}\\ &=1+\frac{3-\sqrt{6+a_n}}{3+\sqrt{6+a_n}}\\ &=1+\frac{3-a_n}{(3+\sqrt{6+a_n})^2}\tag{4} \end{align} $$ From $(3)$, we get $$ \left|\frac{3-a_n}{(3+\sqrt{6+a_n})^2}\right|\le\frac3{(3+\sqrt6)^{n+2}}\tag{5} $$ Therefore, $(4)$ and $(5)$ imply that $$ \begin{align} A &=\lim_{n\to\infty}6^{n+1}(3-a_n)\\ &=18\prod_{k=0}^\infty\frac{6^{k+2}}{6^{k+1}}\frac{3-a_{k+1}}{3-a_k}\\ &=18\prod_{k=0}^\infty\left(1+\frac{3-a_k}{(3+\sqrt{6+a_k})^2}\right)\tag{6} \end{align} $$ converges, and the limit in the question is $\sqrt{A}$.

---

Some Estimates

As $a_n\to3$, $3+\sqrt{6+a_n}\to6$; therefore, we have $$ \begin{align} \frac1{3+\sqrt{6+a_k}}-\frac16 &=\frac{3-\sqrt{6+a_k}}{6(3+\sqrt{6+a_k})}\\ &=\frac{3-a_k}{6(3+\sqrt{6+a_k})^2}\\ &\le\frac{3-a_k}{6(3+\sqrt6)^2}\tag{7} \end{align} $$ and using $(7)$, we get $$ \begin{align} \frac{36}{(3+\sqrt{6+a_k})^2}-1 &=36\left(\frac1{3+\sqrt{6+a_k}}-\frac16\right)\left(\frac1{3+\sqrt{6+a_k}}+\frac16\right)\\ &\le36\frac{3-a_k}{6(3+\sqrt6)^2}\frac2{3+\sqrt6}\\ &=\frac{12(3-a_k)}{(3+\sqrt6)^3}\tag{8} \end{align} $$ For $k\ge n$, $(4)$ and $(2)$ say that $$ \begin{align} \frac{6^{k+1}(3-a_k)}{6^{n+1}(3-a_n)} &=\prod_{j=n}^{k-1}\left(1+\frac{3-a_j}{(3+\sqrt{6+a_j})^2}\right)\\ &\le\exp\left(\sum_{j=n}^{k-1}\frac{3-a_j}{(3+\sqrt{6+a_j})^2}\right)\\ &\le\exp\left(\sum_{j=n}^\infty\frac{3-a_n}{(3+\sqrt6)^{j-n+2}}\right)\\ &=\exp\left(\frac{(3-a_n)3/\sqrt6}{(3+\sqrt6)^2}\right)\tag{9} \end{align} $$ Putting together $(8)$ and $(9)$, for $k\ge n$, we have $$ 1\le\frac{6^{k+1}(3-a_k)}{6^{n+1}(3-a_n)}\frac{36}{(3+\sqrt{6+a_k})^2}=1+O\left(3-a_n\right)\tag{10} $$ where the lower bound is assured by $(4)$ and $(2)$.

---

Correction to Finite Termination

From $(4)$, we have $$ A=6^{n+1}(3-a_n)\prod_{k=n}^\infty\left(1+\frac{3-a_k}{(3+\sqrt{6+a_k})^2}\right)\tag{11} $$ Esimating the product in $(11)$ using $(10)$, we have $$ \begin{align} &\prod_{k=n}^\infty\left(1+\frac{3-a_k}{(3+\sqrt{6+a_k})^2}\right)\\ &=\prod_{k=n}^\infty\left(1+\frac{3-a_n}{6^{k-n+2}}\frac{6^{k+1}(3-a_k)}{6^{n+1}(3-a_n)}\frac{36}{(3+\sqrt{6+a_k})^2}\right)\\ &=\prod_{k=n}^\infty\left(1+\frac{3-a_n}{6^{k-n+2}}(1+O(3-a_n))\right)\\ &=\exp\left(\sum_{k=n}^\infty\left[\frac{3-a_n}{6^{k-n+2}}+O\left(\frac{(3-a_n)^2}{6^{k-n+2}}\right)\right]\right)\\ &=\exp\left(\frac{3-a_n}{30}\right)\left(1+O(3-a_n)^2\right)\tag{12} \end{align} $$ Thus, although we can get from $(4)$ that $$ A=6^{n+1}(3-a_n)+O(3-a_n)\tag{13} $$ we get from $(12)$ that $$ A=\exp\left(\frac{3-a_n}{30}\right)6^{n+1}(3-a_n)+O(3-a_n)^2\tag{14} $$ Therefore, the correction in $(14)$ essentially doubles the number of digits known for $A$.

---

Example $$ \begin{align} e^{(3-a_{20})/60}&=1.000000000000000015342412876422776327920\\[4pt] \sqrt{6^{21}(3-a_{20})}&=4.493767376985934399460882507579755317836\\ e^{(3-a_{20})/60}\sqrt{6^{21}(3-a_{20})}&=4.493767376985934468406116975897359789186\\ \lim_{n\to\infty}\sqrt{6^{n+1}(3-a_n)}&=4.493767376985934468406116975897362358095 \end{align} $$ The error correction adds about $17$ correct decimal places to the estimate for $n=20$.

Answer 2

This is still pretty far from an explicit answer, but it includes some theoretical musings and pretty pictures and, really, isn't that all anyone could ask for? (I also establish the convergence of a class of similar values, but the other answers would likely suffice for that too)

We are considering the sequence of functions, for a fixed $x$ of $$f_n=(2x)^n\left(x-\underbrace{\sqrt{(x^2-x)+\sqrt{(x^2-x)+\ldots+\sqrt{x^2-x}}}}_{n\text{ square roots}}\right)$$ and the limit $f=\lim_{n\rightarrow\infty }f_n$. The question, can be seen to be asking for the value of $\sqrt{6f}$ where $x=3$. This $f$ was chosen since the fixed point of $\lambda\mapsto \sqrt{x^2-x+\lambda}$ is at $x$ and has derivative $\frac{1}{2x}$ at that point, and so we would expect that the value in the nested radicals is $x-O(\frac{1}{(2x)^n})$.

Given that each $f_n$ is quite obviously algebraic, it makes sense to ask about the algebraic properties of $f_n$. In particular, it is quite obvious that, if we basically undo then redo various operations, that $$(2x)^{n-1}\left(x^2-\left(x-\frac{f_n}{(2x)^n}\right)^2\right)=f_{n-1}$$ which, remarkably, simplifies to $$f_n\left(1-\frac{f_n}{(2x)^{n+1}}\right)=f_{n-1}.$$ Suppose we define $Q_n(\lambda)=\lambda\left(1-\frac{\lambda}{(2x)^{n+1}}\right)$. It follows that, if we let $$P_n=Q_1\circ Q_2 \circ \ldots \circ Q_n$$ then it follows that $$P_n(f_n)=f_0=x.$$ What's very interesting is that the limit $P(\lambda)=\lim_{n\rightarrow\infty} P_n(\lambda)$ exists and is holomorphic, which is easily derived from the fact that each $\lambda-Q_n(\lambda)$ grows exponentially small with $n$. What's this mean?

Well, first notice that the roots of $P_n(\lambda)-x$ are exactly the values of the form $$(2x)^n\left(x\pm\underbrace{\sqrt{(x^2-x)\pm \sqrt{(x^2+x)\pm\ldots \pm\sqrt{x^2+x}}}}_{n \text{ square roots}}\right)$$ where each $\pm$ is chosen independently (giving $2^n$ real roots). Of these roots, it is clear that $f_n$ is the least root. Furthermore, it is clear that, since around each root the derivative does not vanish, if we take the set of all roots to the $P_n$, then the set of accumulation points thereof is exactly the zeros of $P$ - meaning that $f$ is the least zero of $P$. So, what does $P$ look like for $x=3$? Well, here's the part with the pretty pictures I mentioned:

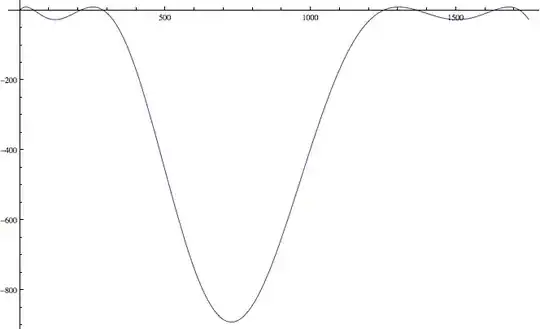
and a plot of $\log(10-P(\lambda))$ (since the range of $P$ is $(-\infty,9]$, as will be seen later)):

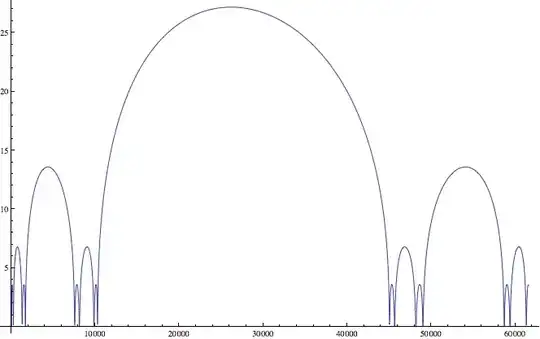
Admittedly, we are only interested in the first time this function crosses $3$, which happens near $0$, but $P$ kind of looks like a line in that domain and that's not as interesting. Also, these bigger pictures illustrate some suspicious properties of $f$ - notice that, from the log plot, $P(6\lambda)$ seems to be around $P(\lambda)^2$ - and there's some sort of fractal behavior going on. That's worrying, because if we want to solve $P(\lambda)=3$, it would be nice if $P$ was expressible in elementary functions, but elementary functions don't usually look like that.

So, how can we get a handle on this $P$ function? Well, recalling that we defined it as a composition of $Q_i$, we see it advantageous to expand the $Q_i$ terms. In particular, define two new functions, $M$ and $Q$ defined as $$M(\lambda)=2x\lambda$$ $$Q(\lambda)=\lambda(1-\lambda).$$ Then, it follows from simple computation that $Q_n=M^{n+1}\circ Q \circ M^{-n-1}$ and since we have cancellations like the following: $$Q_{n-1}\circ Q_{n}=M^{n}\circ Q \circ M \circ Q \circ M^{-n-1}$$ we can write, after substituting and canceling: $$P_n=\underbrace{M^2\circ Q \circ M \circ Q \circ \ldots Q \circ M^{-n-1}}_{n \text{ repetitions of } Q}.$$ This identity is remarkable because it means we can write out a recurrence for $P_n$ as follows: $$P_{n+1}=M^2\circ Q \circ M^{-1} \circ P_n \circ M^{-1}.$$ This is really significant because, the map $g\mapsto M^2\circ Q\circ M^{-1} \circ g \circ M^{-1}$ is continuous under the norm, for any $k$ $$||g||=\sup_{-k\leq x\leq k}g(x)$$ and given that the sequence $P_n$ is convergent under this norm we get the following result: $$P=M^2\circ Q \circ M^{-1} \circ P \circ M^{-1}$$ or, if we write it out without composition, we get $$P(\lambda)=P\left(\frac{\lambda}{2x}\right)\left(2x-P\left(\frac{\lambda}{2x}\right)\right).$$ Moreover, since each $Q_n$ has $Q_n(0)=0$ and $Q_n'(0)=1$, and $P$ is holomorphic, we get that $P(0)=0$ and $P'(0)=1$ - and this, along with the functional equation above, uniquely determines $P$. Moreover, this implies that for $x>1$, the function $P$ has attains a maximum of $P(\lambda)=x^2$ and hence, by the intermediate value theorem, for any $x>1$, there is a solution to $P(\lambda)=x$ and thus $f$ converges.

This doesn't seem to yield an easy solution for $x=3$, but maybe someone else has some brilliant solution (although we've decidedly wandered into chaos theory since a general solution to $P$ would also allow quick calculation of iterates of the logistic map). If $x=2$, we actually have a nice closed form for $P$ which is $P(\lambda)=2-2\cos(\sqrt{\lambda})$, the solution set thereof being easy to find and implying that $\sqrt{4f}=\pi$, as anticipated. Also, for $x=1$, we have $P(\lambda)=1-e^{-\lambda}$, which has no solutions to $P(\lambda)=1$, since the series for $f$ wouldn't converge there anyways. I'm not sure that this yields any hints as to the form of $P$ with $x=3$, but maybe a Fourier transform of $P(\lambda)$ or $P(\lambda^2)$ or $P(\lambda^3)$ would be enlightening.

The only other theoretical progress I have is that, since $P$ is holomorphic, we can write out an analytic expansion (which has infinite radius of convergence) $$P(\lambda)=a_0+a_1\lambda+a_2\lambda^2+a_3\lambda^3+\ldots$$ which has $a_0=0$ and $a_1=1$, and, by applying the functional equation and moving terms around yields that $a_i$ can be calculated as $$a_n=\frac{1}{2x-(2x)^n}\sum_{i=1}^{n-1}a_ia_{n-i}$$ which doesn't seem to have a nice closed form, sadly. The first few terms of the Taylor series of $P$ for $x=3$ are $$P(\lambda)=\lambda -\frac{\lambda ^2}{30}+\frac{\lambda ^3}{3150}-\frac{11 \lambda ^4}{8127000}+\frac{97 \lambda ^5}{31573395000}+O(\lambda^6)$$

Answer 3

This isn't an answer since I have no proof, but numerically it appears that

$$ \lim_{n\to\infty} 6^{n/2} \underbrace{\sqrt{3-\sqrt{6+\sqrt{6+\dotsb+\sqrt{6}}}}}_{n\text{ square root signs}} = 1.83457284939678559111564141519063\ldots $$

Here's the Mathematica code I used to calculate this:

s[n_] := Module[{start = Sqrt[6]}, For[j = 1, j < n, j++, start = Sqrt[6 + start] ]; Return[start] ]; m = 50; 6^(m/2) Sqrt[3 - N[s[m], 100]]

Answer 4

This completes Slade's idea: For $t>2$, let $k=t^2-t$ and $$b_n=\underbrace{\sqrt{k+\sqrt{k+\cdots+\sqrt{k}}}}_{n}.$$ Then $b_n\uparrow t$. We are interested in the sequence $$a_n=(2t)^n(t-b_n).$$ Slade pointed out that $$a_n-a_{n-1}=(2t)^{-n-1}a_n^2.\tag{1}$$ On the other hand, $$b_n^2=k-b_{n-1}=t^2-t+b_{n-1}.$$ That gives $$t-b_n=(t-b_{n-1})\frac{1}{t+b_{n}}<\frac{t-b_{n-1}}{t}.$$ So $t-b_n<Ct^{-n}$ for some constant $C$. That means $$a_n<C2^n.\tag{2}$$ Substitute (2) to the RHS of (1) we get $$a_n-a_{n-1}<C^2(2t)^{-n-1}2^{2n}=\frac{C}{t}(t/2)^{-n}.$$ Since $t>2$, it follows that $a_n$ is bounded.

Note: Since we obtained (2) by a very crude estimation, we can improve the lower bound for $t$ a lot. I believe with a careful computation that can be pushed to $1$.

Note 2: I just realized that the question is for the actual limit, which is not obvious (if possible) from this calculation.

Answer 5

Here are some useful calculations. I might turn them into a solution later, but I've run out of time for the moment, and thought I'd post them as-is.

---

Fix $t>1$, and set $k=t^2 - t$.

Let $a_n = (2t)^n (t - \underbrace{\sqrt{k + \sqrt{k + \cdots}})}_{n}$. We have $a_0 = t$, and the following recurrence:

$$a_n - a_{n-1} = (2t)^{-n-1}a_n^2$$

So the sequence is increasing. If we can show that it is bounded, then the above equation implies that the differences shrink exponentially, so $\lim_{n\to\infty} a_n$ exists.

Answer 6

I'm only addressing the question of convergence here.

This is probably off by one or two factors of $6$, but I think it gets the idea across:

$$\begin{align} {1\over a_n^2}&={1\over6^n}{1\over3-\sqrt{6+\sqrt{6+\cdots}}}\\ \\ &={1\over6^n}{3+\sqrt{6+\sqrt{6+\cdots}}\over3^2-(6+\sqrt{6+\cdots})}\\ \\ &={1\over6^n}{3+\sqrt{6+\sqrt{6+\cdots}}\over3-\sqrt{6+\cdots}}\\ \\ &={1\over6^n}\left(3+\sqrt{6+\sqrt{6+\cdots}} \right)\left(3+\sqrt{6+\cdots} \right)\cdots\left(3+\sqrt{6} \right)\\ \\ &=\left(6-(3-\sqrt{6+\sqrt{6+\cdots}})\over6 \right)\left(6-(3-\sqrt{6+\cdots})\over6 \right)\cdots\left(6-(3-\sqrt{6})\over6 \right)\\ \\ &=\left(1-{3-\sqrt{6+\sqrt{6+\cdots}}\over6}\right)\left(1-{3-\sqrt{6+\cdots}\over6}\right)\cdots\left(1-{3-\sqrt{6}\over6}\right) \end{align}$$

So

$${1\over L^2}=\left(1-{3-\sqrt{6}\over6}\right)\left(1-{3-\sqrt{6+\sqrt6}\over6}\right) \left(1-{3-\sqrt{6+\sqrt{6+\sqrt6}}\over6}\right)\cdots$$

The convergence of the infinite product depends on how quickly $\sqrt{6+\sqrt{6+\cdots}}$ approaches $3$. But

$$\begin{align} 3-\sqrt{6+\sqrt{6+\cdots}} &={3-\sqrt{6+\cdots}\over3+\sqrt{6+\sqrt{6+\cdots}}}\\ \\ &=\left({1\over3+\sqrt{6+\sqrt{6+\cdots}}}\right) \left({1\over3+\sqrt{6+\cdots}}\right)\cdots \left({1\over3+\sqrt{6}}\right)\\ \\ &\lt\left({1\over3}\right)\left({1\over3}\right)\cdots\left({1\over3}\right)={1\over3^n} \end{align}$$

which is enough to show the product converges.