4

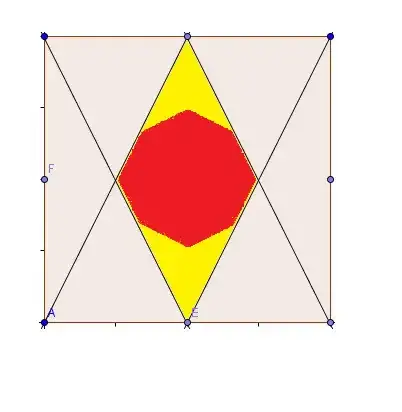
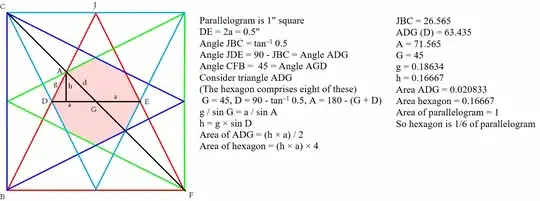
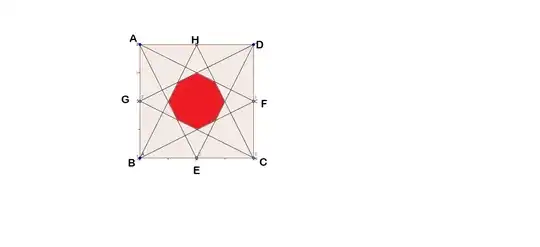
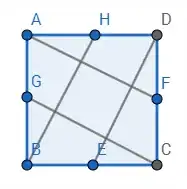
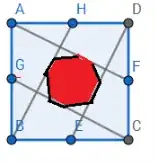
The following picture is constructed by connecting each corner of a square with the midpoint of a side from the square that is not adjacent to the corner. These lines create the following red octagon:

enter image description here

The question is, what is the ratio between the area of the octagon and the area of the square. One is supposed to find the solution without a ruler.

By removing some lines, I find it easy to see that the ratio between the yellow area and the square is 1/4. But I am not sure if this helps.

enter image description here

Adam
  • 3,679
  • 2
    You might want to find the area of, say, the upper right quadrant. The top and right points are $(1/2, 0)$ and $(0, 1/2)$. The top-right point is at ... well, it's on the line $y+2x= 1$ and $x + 2y = 1$ (by symmetry), so it's at $(1/3, 1/3)$. Now it's pretty easy. (BTW, I'm assuming your original square goes from $-1$ to $1$ in $x$ and $y$. Since all you need is the ratio, this assumption does no harm.) – John Hughes Oct 17 '14 at 15:39

4 Answers4

3

I think the following image will say more than any text. You can divide the image into smaller squares that will allow you immediately to calculate the ratio.

The ratio of the red area within the whole square is the same as the red area in the big green square to the area of the whole green square. And this is (counting in units of the 9 small squares): $(1+1/4+1/4) : 9 = 1.5 : 9 = 1:6$.

drawing

flawr
  • 16,533
  • 5
  • 41
  • 66
  • To create the image you had to use that the intersection point is at (-1/3,1/3) as calculated by John right? – Adam Oct 17 '14 at 17:04
  • Yes, this fact is obvious when you extend the the fine square grid to the rest of the image. – flawr Oct 17 '14 at 17:09
  • @flawr,thanks for sharing this answer.I'm interested to know that do you have any idea about why that red filled small square with green sides will have $\frac{1}{9}$ area of green sided square? I want to prove this in euclidean geometry but I can't find a way to show it will become $\frac{1}{9}$ – user2838619 Oct 20 '14 at 13:03
  • If I understood you correctly that's pretty simple: We have 9 small green squares, so one of those has $1/9$ of the area of the whole big green square. Is that what you were asking? – flawr Oct 20 '14 at 13:10
  • thanks for reply .No, i think i explained it bad.My question is about the construction.in your answer,you used the fact that 2 of the lines which construct that $\frac{1}{9}$ squares goes trough one corners of octagon.why this happens? – user2838619 Oct 20 '14 at 13:18
  • Ah, the construction of the square didn't use this. The big green square has half the sidelength of the whole image, and the small squares have the sidelength of $1/3$ of the green square. But the corner of the octagon is indeed exactly on the corner of that square. This is because the lines that intersect there have the slope $2$ and $1/2$. This means if you go from the point $F$ two small steps to the right, you have to go one up. (And similarly with the other line.) Is that clear? – flawr Oct 20 '14 at 13:22
  • thanks,just one thing remains that i don't get. why that octagon corner will be reached when we go two steps to right and on to up from $F$? – user2838619 Oct 20 '14 at 13:31
1

A calculated answer. Maybe not the simplest.

enter image description here

Xander Henderson
  • 29,772
user514455
  • 11
0

Let us name all the points on the outer square like this:

enter image description here

So, AB, CD, EF, AD are side of the square of length say $\mathrm{a}$ and E, F, G and H are midpoints of the sides of the square. Now consider line segments AF, GC, BH, ED. AF and GC intersect BH and ED to form another square.

enter image description here

The area of this square is $\frac{a^2}{5}$ as proved from answers to this question. So, side of this square is $\frac{a}{\sqrt{5}}$. The sides of the square act as span of the octagon (S).(See octagon).

enter image description here Line HC, AE, GD, FB not drawn for clarity.

Area of octagon in terms of span = $\mathrm{2(\sqrt{2}-1)S^2 = 2(\sqrt{2}-1)\frac{a^2}{5} = \frac{2(\sqrt{2}-1)}{5}{a^2}}$

Therefore, ratio between the area of the octagon and the area of the square = $\mathrm{\frac{2(\sqrt{2}-1)}{5}}$

Shadow
  • 105
  • 5
-1

I was frustrated by the solution being 1/6 because that is not the result if one calculates the area of a regular octagon with a radius that is L/4, where L is the length of large square.

The gridded image above makes clear that red shape is close to, but not actually, a regular octagon.

Instead, the horizontal distance from the center of the large square to a vertex is 1.5 times the length of the smallest green square. The angled distance from the center of the large square to a vertex is 'sqrt(2)' times (not 1.5 times) the length of the smallest green square. The vertices do not lie on a circle, so it is not a regular octagon (with equal all the included angles being equal), even though the lengths of all the sides are equal.

Bob
  • 11