3

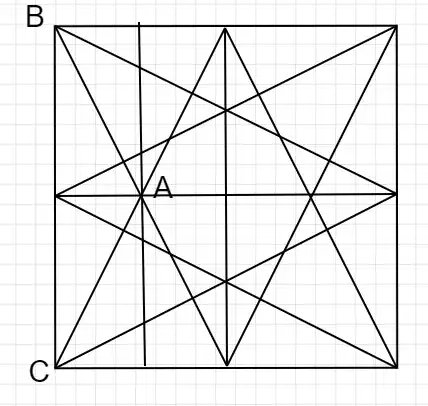
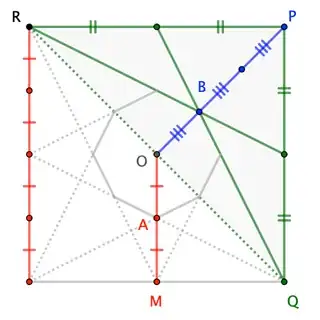
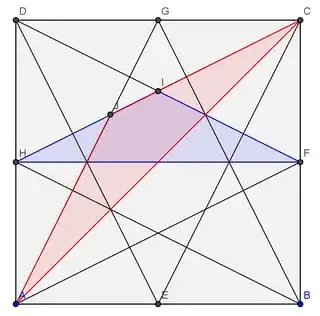
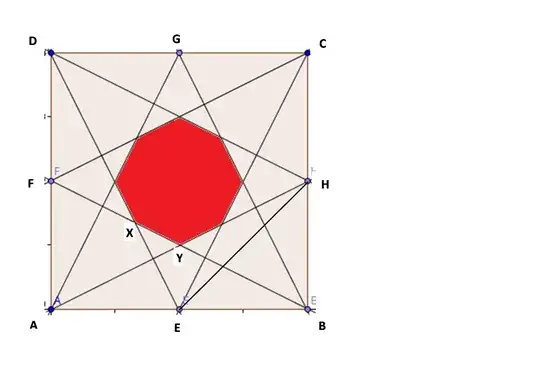
I stumbled upon this old question "Area of octagon constructed in a square" that involves finding the area of an octagon within a square as shown:

enter image description here

I found that the octagon is not regular. So, my question is this:

Prove that the octagon shown above is not regular, assuming the only length we are initially given is the side length of the square.

Note: The edges of the octagon are determined by the line joining the vertices of the square to midpoints of the square's sides.

So far, the easiest way I could think of was to use the cosine rule to get the largest angle in $\triangle ABC$ (below) and show that the total of the angles would not be equal to the expected sum of a regular octagon.

enter image description here

Are there any other ways of proving that this octagon is not regular?

Community
  • 1
user183756
  • 33
  • 1
    Looking at it, the octagon is cut out from a rotated square by removing 4 of the smallest pictured triangles. These triangles are obviously all congruent, so the octagon has all side lengths the same. However it is not regular, since these small triangles are not isosceles, so the segments of the octagon on the rotated square are not centered. – Cheerful Parsnip Feb 18 '20 at 01:21
  • The octagon is regular as result of the symmetry. The angles of it are 135. I think that you will fail to prove that it is not regular. – Moti Feb 18 '20 at 08:06
  • Some basic trigonometry on a $1,2,\sqrt{5}$ triangle will tell you all the angles you need and will prove that the angles are not all $135^\circ$. Incidentally, the side length of the square is irrelevant. The important fact is that it is a square. – nickgard Feb 18 '20 at 08:53
  • 1
    @moti It is definitely not regular. You don't have full rotational symmetry. The angles come in congruent sets of 4. – Cheerful Parsnip Feb 18 '20 at 18:11

3 Answers3

2

enter image description here

$$\underbrace{|OA| = \frac12|OM|}_{\text{$A$ is the midpoint of $\overline{OM}$}}=\;\; \frac14|PQ| \;\;\color{red}{\neq}\;\; \frac13\cdot\frac1{\sqrt{2}}|PQ| \;\;= \underbrace{\frac13|OP| = |OB|}_{\text{$B$ is the centroid of $\triangle PQR$}}$$

Blue
  • 75,673
2

Here is a better way that requires absolutely no calculation at all.

octagon in square with two isosceles triangles each of which comprises a diameter and two sides of the octagon

If the octagon is regular, then rotating the blue triangle would yield the red triangle, but clearly the blue triangle has the shorter long side.

user21820
  • 57,693
  • 9
  • 98
  • 256
1

A regular octagon has all its exterior angles equal, so to demonstrate non-regularity it suffices to show that there are two exterior angles which are not equal to each other. In the diagram below we focus on showing that $\angle EXB <\angle AYF$. enter image description here Given that $ABCD$ is a square and $E,F,G,H$ are midpoints, we can infer that $EB=BH=\frac{1}{2}AD$ and hence, using Pythagoras' Theorem, $EH=\frac{\sqrt{2}}{2}AD$ so that $EH < AD$.

Focusing now on $\triangle EDH$ and $\triangle AHD$, we have $ED=DH=AH$, so both are isosceles and their equal sides are the same. Hence, since $EH < AD$, $\angle EDH < \angle AHD$.

Since $F$ and $H$ are mid-points of sides $AD$ and $BC$ respectively of the square, $BF$ and $HD$ are parallel, and so $\angle EXB = \angle EDH$ and $\angle AYF = \angle AHD$. Hence:

$$\angle EXB = \angle EDH < \angle AHD = \angle AYF$$

QED

Adam Bailey
  • 4,197