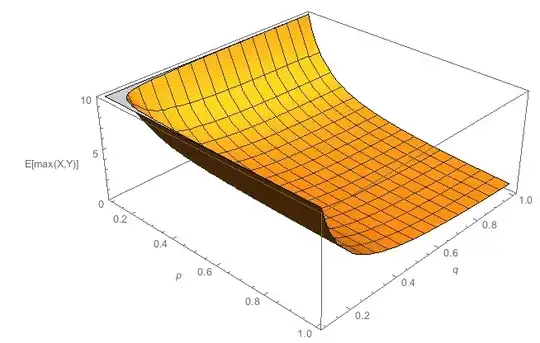
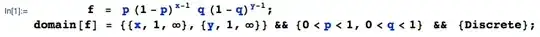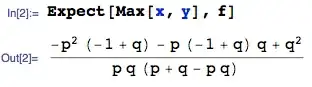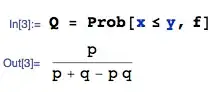Let $X,Y$ be independent geometric random variables, where $X$ has parameter $p$ and $Y$ has parameter $Q$. What is $E[\max(X,Y)]$, and what is $E[X\mid X\leq Y]$?
If we follow the definition of expectations, $E[\max(X,Y)]$ would be $$\sum_{k=1}^\infty k\cdot Pr(\max(X,Y)=k)=\sum_{k=1}^\infty k\cdot [Pr(X=k)Pr(Y\leq k)+Pr(X\leq k)Pr(Y=k)-Pr(X=k)Pr(Y=k)]$$ which is quite messy to compute. Is there an easier way?
(Similar question for computing $E[X\mid X\leq Y]$.)
If $T=\min \{X,Y\}$, then $T$ is a Geometric random variable with parameter $p+Q-pQ$. We can write $Z=X+Y-T$. So
$E[Z]=E[X]+E[Y]-E[T]=\frac{1}{p}+\frac{1}{Q}-\frac{1}{p+Q-pQ}$
Hint: Let $Z = \max(X,Y)$. Then $$P[Z \leq z] = P[\max(X,Y) \leq z] = P[X \leq z,Y\leq z]$$ This is because $\max(a,b) \leq z \iff a \leq z, b\leq z$
As for $E[X|X \leq Y]$,consider first $E[X|X \leq y]$. You have to compute the conditional pmf and work with that. Let me know if you have difficulties with this in comments. If so, I will update my answer.
Let $X \sim Geometric(p)$ and $Y \sim Geometric(q)$ where $X$ and $Y$ are strictly positive independent random variables. Then $(X,Y)$ have joint pmf $f(x,y)$:
Part 1: You seek:
where I am using the Expect function from the mathStatica package for Mathematica to do the nitty-gritties.
Here is a plot of the solution $E[max(X,Y)]$, as parameters $p$ and $q$ vary:
Part 2: $E[X \, | \, X \leq Y]$
Let $g(x,y)$ denote the conditional joint pmf:
$$g(x,y) = f\big((x,y) \, | \, X \leq Y\big) = \frac{f(x,y)}{P(X \leq Y)}$$
The denominator $Q = P(X \leq Y)$ is:
Thus, the conditional joint pmf $g(x,y)$ is:
Since we know the conditional pmf $g(x,y)$ ... it is straightforwards to calculate the conditional expectation $E_f[X \, | \, X \leq Y] = E_g[X]$ as:
Notes
