When simplifying $\sin(\arctan(x))$, why is negative $x$ not considered?

Question

Let $u = \arctan(x)$, hence $x = \tan(u)$ for $u$ belongs in $(-\frac\pi2, \frac\pi2)$. Since $u$ belongs in $(-\frac\pi2, \frac\pi2)$, we consider $\sin(u)$ where $u$ belongs in $(-\frac\pi2, \frac\pi2)$.

I used the unit circle to determine that the hypotenuse is $\sqrt{x^2 + 1}$ and got an answer $\sin(u) = \frac{x}{\sqrt{x^2 + 1}}$ when I consider than the angle $u$ lies between $(0, \frac\pi2)$.

That's what my textbook says too. However, why don't we also consider when $x$ is negative, and the angle $u$ lies between $(-\frac\pi2, 0)$ ?

Answer 1

An angle $\theta$ is said to be in standard position if its vertex is at the origin and its initial side lies on the positive $x$-axis.

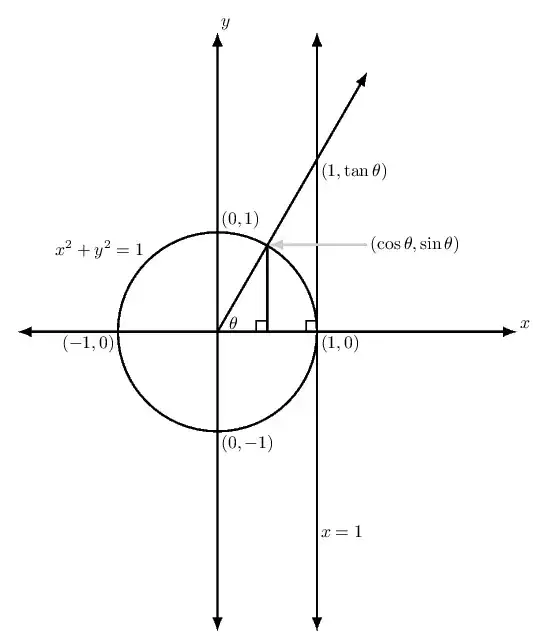
The unit circle is the circle with radius $1$ and center at the origin of the coordinate plane.

We define the cosine and sine of an angle in standard position to be, respectively, the $x$-coordinate and $y$-coordinate of the point where the terminal side of the angle intersects the unit circle. We define the tangent of an angle in standard position to be the $y$-coordinate of the point where the terminal side of the angle intersects the line $x = 1$. See the diagram below.

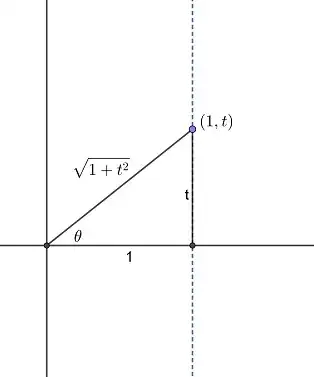
If $\theta = \arctan x$, then $\tan\theta = x$ and $-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}$. Consequently, we can draw a right triangle in the first quadrant or fourth quadrant, as shown below.

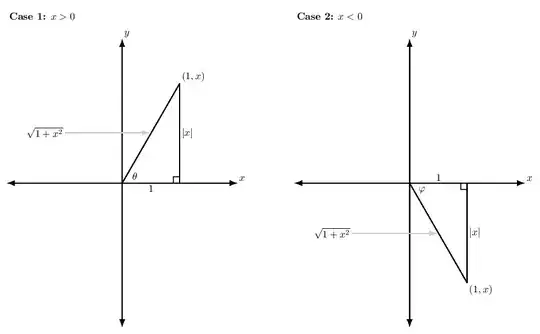
If $x > 0$, we draw a right triangle in the first quadrant with opposite side of length $|x| = x$, adjacent side of length $1$, and hypotenuse of length $\sqrt{1 + x^2}$.

If $x < 0$, we draw a right triangle in the fourth quadrant with opposite side of length $|x| = -x$, adjacent side of length $1$, and hypotenuse of length $\sqrt{1 + x^2}$.

If $x = 0$, we draw the line segment from $0$ to $1$ on the positive $x$-axis. The opposite side has length $|x| = |0| = 0$, the adjacent side has length $1$, and the hypotenuse has length $\sqrt{1 + x^2} = \sqrt{1 + 0^2} = \sqrt{1} = 1$.

In each case, the terminal side of the angle intersects the line $x = 1$ at the point $(1, x)$ (yes, I am using $x$ in two different ways here), so the tangent of the angle is $x$.

We find the sine of the arctangent of $x$ by dividing the $y$-coordinate of the point $(1, x)$ by its distance from the origin. Hence, in each case,

$$\sin[\arctan(x)] = \frac{x}{\sqrt{1 + x^2}}$$

Note that since the denominator is always positive, the sign of $\sin[\arctan(x)]$ is equal to the sign of $x$.

Since the numerator of $\sin[\arctan(x)]$ is the $y$-coordinate of the point $(1, x)$ rather than the length of the side opposite angle $\theta$, we obtain the same result when we draw the triangle in the fourth quadrant as we do if we draw it in the first quadrant.

Answer 2

Draw the right angle triangle.

Opposite side = x, adjacent side = 1, hypotenuse= $\sqrt{1+x^2}$, so

$$ \sin(...) = \pm \frac{x}{\sqrt{1+x^2}} $$

two signs due to $\sqrt .. $

EDIT1

Why the double sign? $\pm $ It is easy to see. Arctan has two signs. It can be $x$ or $x + \pi $ x>0 Sine of this argunent is positive if in the first quadrant and negative if in the the third. x< 0 Sine of this argunent is negative if in the first quadrant and positive if in the the third. While we are simplifying we have in no way neglected the negative sign.

Answer 3

If $-\frac\pi2\lt u\lt\frac\pi2$, then $\cos(u)\gt0$. Therefore, if $\tan(u)=x$, then $\cos(u)=\frac1{\sqrt{1+x^2}}$.

Thus, if $\arctan(x)=u$, then $$ \begin{align} \sin(u) &=\tan(u)\cos(u)\\ &=\frac{x}{\sqrt{1+x^2}} \end{align} $$ Furthermore, since $\sin(x)$ and $\arctan(x)$ are odd functions, $$ \sin(\arctan(-x))=-\sin(\arctan(x)) $$

Answer 4

Using $x$ in $u = \arctan x$ and then referring to the $xy$-plane causes $x$ to have two different meanings.

Try $\theta = \arctan t$

You can draw a picture of $\theta = \arctan t$ by considering the triangle below with vertices at $(0,0), (1,0), \text{and} \ (1,t)$. The unit circle is unnecessary. Note that the picture implies $\sin \theta = \dfrac{t}{\sqrt{1+t^2}}$, and the sign is handled correctly by the sign of $t$. If your book says otherwise, then it is wrong.

Answer 5

To add some additional information regarding user46234's comment, we can also understand the omission of a $\pm$ sign as a simple consequence of algebra.

Here are the relevant pieces of information to conclude this:

• By definition, $\sqrt{x^2}=|x|$

• $\arctan$ is a strictly increasing function bounded between $(-\frac{\pi}{2},\frac{\pi}{2})$

• $\arctan(0)=0$

• $\sin(x) \geq 0$ if $x \in [0,\frac{\pi}{2})$ and $\sin(x) \lt 0$ if $x \in (-\frac{\pi}{2},0)$

• $\cos(x) \gt 0$ if $x \in (-\frac{\pi}{2},\frac{\pi}{2})$

---

Working forward from the above bulleted points:

Let $y=\arctan(x)$.We know that $y \in (-\frac{\pi}{2},\frac{\pi}{2})$. By definition, $\tan(y)=\tan\circ \arctan(x)=x \implies \frac{\sin(y)}{\cos(y)}=x$

To further simplify, we use the Pythagorean identity $\cos^2(y)+\sin^2(y)=1 \implies \cos^2(y)=1-\sin^2(y)$. Taking the square root of both sides yields: $|\cos(y)|=\sqrt{1-\sin^2(y)}$. Note that $y \in (-\frac{\pi}{2},\frac{\pi}{2})$, which means that $\cos(y) \gt 0$...and therefore $|\cos(y)|=\cos(y)$, so that we have $\cos(y)=\sqrt{1-\sin^2(y)}$.

We then have that $x=\frac{\sin(y)}{\sqrt{1-\sin^2(y)}}$. Rearranging and then squaring gives us $\big(1-\sin^2(y)\big)\cdot x^2=\sin^2(y)$. Because $x=\tan(y)$, we can use the tangent expression of the Pythagorean identity to further simplify: $1+\frac{\sin^2(y)}{\cos^2(y)}=\frac{1}{\cos^2(y)} \implies1+\tan^2(y)=\frac{1}{1-\sin^2(y)} \implies \frac{1}{1+\tan^2(y)}=1-\sin^2(y) \implies\frac{1}{1+x^2}=1-\sin^2(y)$. Note that in order to apply this substitution, we need to make sure that $\cos(y) \neq 0$...however, given that $y \in (-\frac{\pi}{2},\frac{\pi}{2})$, we know that $\cos(y) \neq 0$. We can then apply the relevant substitution that gives us:

$$\frac{x^2}{1+x^2}=\sin^2(y)$$

Taking the square root of this expression gives us:

$$\frac{|x|}{\sqrt{1+x^2}}=|\sin(y)| \quad (\dagger_1)$$

Now, suppose $x \geq 0$. Then $y \in [0,\frac{\pi}{2})$. We then know that $\sin(y) \geq 0$, so we must have that $|x|=x$ and $|\sin(y)|=\sin(y)$. Under these circumstances, $(\dagger_1)$ is just $\frac{x}{\sqrt{1+x^2}}=\sin(y)$.

Next, suppose $x \lt 0$. Then $y \in (-\frac{\pi}{2},0)$. We then know that $\sin(y) \lt 0$, so we must have that $|x|=-x$ and $|\sin(y)|=-\sin(y)$. Under these circumstances, $(\dagger_1)$ is $\frac{-x}{\sqrt{1+x^2}}=-\sin(y)$, which can of course be rewritten as $\frac{x}{\sqrt{1+x^2}}=\sin(y)$.

Thus, across all relevant cases, we must have that $\sin(\arctan(x))=\sin(y)=\frac{x}{\sqrt{1+x^2}}$