1

I was thinking about this problem yesterday and was wondering if someone can provide some insight into it.

Let's say we have two points in Euclidean space: $p_1$ at $\left(0, 0\right)$ and $p_2$ at $\left(1, 1\right)$.

When considering the path between these two points, we can visualize the $L_2$-norm as a straight line between the two points and the $L_1$-norm as a two-line segment that contains a segment along the x-axis of length 1 followed by a segment along the y-axis of length 1.

Additionally, you can represent the path where you take smaller step-sizes, such as 0.5, such that you create a multi-segmented line. Below is an illustration of $k=1\dots16$.

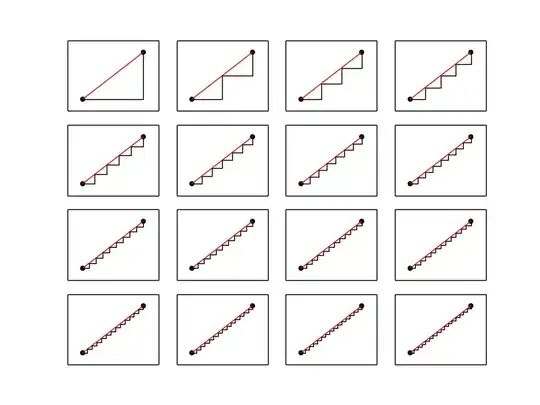
paradox-tiles

However, this multi-segmented line still has length of 2. This brings up the first question:

  1. Why is it if you were to take the limit as $k \rightarrow \infty$, the multi-segmented line appears to converge on the target line, but the length is still of length 2?

There's the intuitive answer of "duh", but why can't you express the length of the the line as a limit or integral? The area between the two lines appears to converge to zero, but the length of our approximation is still of length 2.

This leads into the more interesting question of:

  1. Is there a name for this question / paradox?

I'm really curious if there are any examples of this paradox in the physical sciences, where attempts to "approximate" a line integral using orthogonal components fails to converge on the actual solution.

Thanks!

Stefan Novak
  • 123
  • The problem is that of dimensionality, you are approximating a two dimensional object by two 1 dimensional objects. At some point as you shrink the step size you must switch between the 1 and 2 dimensions. This is a first order transition because it is discontinuous. As for examples in the physical sciences you can look to materials science and many body systems which undergo high dimension transitions that are discontinues (glassy transition, some melting transitions, magnetic transitions in iron). – Adam Cadien Oct 02 '14 at 19:33
  • 2
    Related: Is value of $\pi=4$? – epimorphic Oct 02 '14 at 19:38
  • 1
    @epimorphic: Ah! Good find. I do like what robjohn had to say: "not all approximations that look good are good. We always MUST prove that the errors in our approximations go to zero." – Stefan Novak Oct 02 '14 at 19:53
  • It appears you are dealing with the inverse of the problem of fractal dimension encountered when measuring coastlines but I'll leave it to the mathematicians to state exactly how that relates to the subdivided L1 norm. Note that the area between between the lines is always $\frac{1}{2k}$ so it indeed does converge to zero. – bogatron Oct 02 '14 at 21:56

1 Answers1

0

The area between the two lines appears to converge to zero, but the length of our approximation is still of length 2.

The area between the curves does indeed converge to zero, but since you can fit an infinite length into an infinitesimal area, this does not impose a bound on the length error.

MvG
  • 42,596
  • Ah! Great point. I think that this observation along with the notion that "not all approximations that look good are good" answers the question. Thanks for the concise answer! – Stefan Novak Oct 06 '14 at 17:52