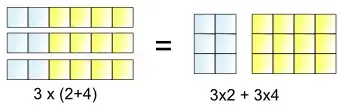
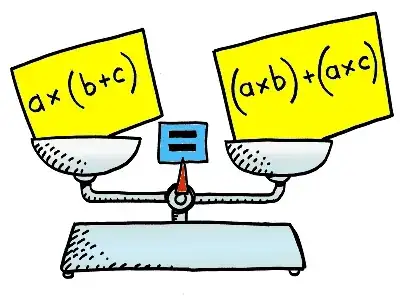
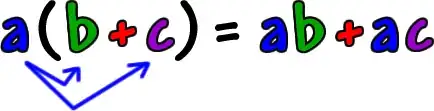10

Suppose I have this expression that needs to be simplified:

$$4(2x + 4)$$

It can be simplified down to this:

$$8x + 16$$

In this case, this expression has been simplified down using the distributive property. My question is, how exactly does the number, in this case, $4$, get distributed to the two numbers in the parentheses? Why exactly does the distributive property work?

Ethan Bierlein
  • 1,242

6 Answers6

27

Check out this page.

I think the picture there is worth a thousand words.

enter image description here

user26486
  • 11,331
G Tony Jacobs
  • 31,218
  • there is a similar diagram with some exercises at this link http://mathuprising.comlu.com/distributive-property.html – John Joy Sep 15 '14 at 18:20
18

For most people, the fact that the $\text{LHS}$ and $\text{RHS}$ weigh the same is proof enough.
I'm glad that you're not that people. Distrubution

Let's see an example of distribution of multiplication over addition of integers: $$ \begin{align} 3\times\left(\color{red}{1} + \color{blue}{2}\right) &= \color{red}{3} + \color{blue}{6}\\ 3 \times \left(\color{red}{\star}\space\color{blue}{\star\star}\right) &= \begin{array}{cc} \color{red}{\star} &\color{blue}{\star\star} \\ \color{red}{\star} &\color{blue}{\star\star} \\ \color{red}{\star} &\color{blue}{\star\star} \end{array} \end{align} $$

Multiplication can elementarilly defined as:

$$a\times b = \sum_{i=1}^{a} b $$

So, even when we have $n$ variables, this still applies. $$k\times (x_1 + x_2 + \dots + x_n)= k\times\sum_{i = 1}^{n}x_i = \sum_{j = 1}^{k} \sum_{i = 1}^{n}x_i$$

Hence giving the illusion of distribution:

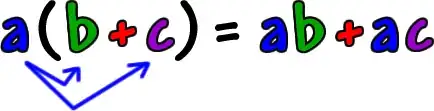
illusion

All that's happening here is this:

$$ \begin{align} a\times(b+c) &= (b+c) + (b+c) + (b+c) + \dots \text{a times}\\ &= (b+b+b+\dots \text{a times}) + (c+c+c+\dots \text{a times})\\ &= (a\times b) + (a\times c) \end{align}$$

@MathLove has used this fact to note the result of the example you've given.

Note: The definition I gave of multiplication gets shaky for non-whole numbers. In which case, you turn to the geometrical interpretation of multiplication as the Area of a Rectangle
Community
  • 1
Nick
  • 6,804
  • 1
    Actually, that answer is very good. I would have gonne forward in your proof of distribution with the sum, by switching the two finite sums that are independant! – Saffron Sep 16 '14 at 10:35
12

Note that $$\begin{align}4(2x+4)&=(2x+4)+(2x+4)+(2x+4)+(2x+4)\\&=(2x+2x+2x+2x)+(4+4+4+4)\\&=4\times (2x)+4\times 4.\end{align}$$

mathlove
  • 139,939
  • 22
    Lucky that $4$ was an integer. – Nick Sep 15 '14 at 13:11
  • 1
    @Nick the distributive property of rationals can be derived from integers, and then reals from rationals, partly due to how they are constructed. In a sense, rationals/reals are certain extensions of the natural numbers (parts of them act like natural numbers) that obey nice properties, like distributivity, because we want them to. "Because we made it so" is, however, less interesting. ;) (The naturals, naturally, are not "made" but "found", if you believe that pithy quote) – Yakk Sep 15 '14 at 20:22
3

I would say "the reason" is works is that, at least when you look at just the natural numbers, multiplication is repeated addition. See mathlove's answer which uses this definition for an idea of how it works. You could generalize this to a proof for $n(a+b)=na+nb$ using induction on $n$.

To expand to the integers, the rationals, the reals, etc. you would want to look at how you construct them from the natural numbers, and see that the distributive law carries over through the construction.

R.. GitHub STOP HELPING ICE
  • 616
  • ... or you might assert it axiomatically of the reals, perhaps based on a dissection of rectangles, and only worry about a particular construction of the reals (i.e. whether your theory actually has a model) some years later in your education. – Steve Jessop Sep 15 '14 at 17:30
  • @SteveJessop: Are you referring to the visual "proof" in the answer by G Tony Jacobs, or some other method with rectangles? I'd hesitate to recommend anything like that since there are a number of pseudo-proofs of false statements using similar visual approaches. I seem to recall there being a nice question on this site with examples but I don't have the link handy. – R.. GitHub STOP HELPING ICE Sep 15 '14 at 18:10
  • 1
    I mean that because of the intuition inspired by rectangles (and the known theorem for integers) you choose to make distributivity an axiom of the reals (indeed, of any field). Visual pseudo-proofs are particularly cunning because people don't learn geometry any more and therefore have predictable weaknesses when it comes to assessing them, but anyway I don't mean that the image needs to be a proof, just that it motivates the axiom. – Steve Jessop Sep 15 '14 at 20:09
0

a(b+c)=ab+ac: This is the distributive property.

a(b+c)=ab+ac

a(b+c)= a(b+c): All I did here is factor out the "a"

You are left with a true statement. a(b+c) will always equal a(b+c) because something will always equal itself. If a(b+c)=ab+bc is the distributive property, and I just simplified the distributive property down to a true statement, then the distributive property must equal the true statement because simplifying something does not change its value. So since the true statement equals the distributive property, then the distributive property must always be true because the true statement will always be true.

Akash Muthu
  • 1
0

$$a(b+c)$$ $$=a(\frac {ba}{a} +\frac {ca}{a})$$ $$=a(\frac {ba+ca}{a})$$ $$=ba+ca$$

$$\therefore a(b+c)=ba+ca$$

AltercatingCurrent
  • 635