Why does the geometric interpretation of the distributive law make sense

Question

I am a 4th grade student and just have a maths question.

I was looking at the distributive law: https://en.wikipedia.org/wiki/Distributive_property

On this website they have a geometric interpretation. My problem is this: Isn't area defined? Like the space enclosed by a square is not actually $x^2$ units squared, it's just what we say it is. Hence my problem with the visualization of fraction multiplication in terms of "area" as well.

Could anyone please clear this up? I am interested into why the mathematics works.

Thank you.

Answer 1

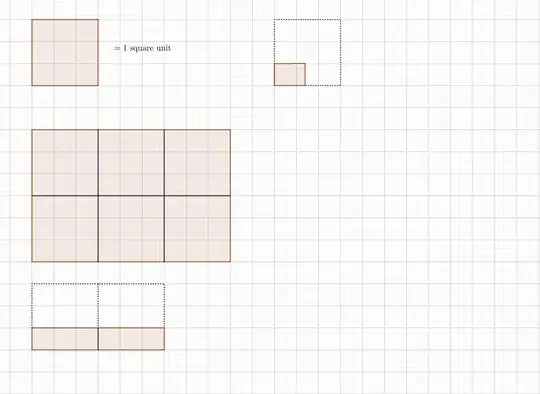
I think you are confused by this fact;

How does multiplication correspond to area?

1: This is simple. When we multiply two numbers, $a$ and $b$, we can think of it as a rectangle with side $a$ and side $b$. This is because of the rectangle area formula $A = lb$ corresponds to direct multiplication. The important thing to note is that, at the standpoint of rectangles, $a \text{ units } \times b\text{ units } = c\text{ units}^2$. Remember that we are measuring the rectangle area in square units. This really means that the product of two values (sides) corresponds to a product (square units).

Theoretically, you could even do it with a parallelogram (if you know what it means). However, we use rectangles in most visualizations as it is simplest.

In the same way, multiplying a number by itself corresponds to the area of a shape with equal sides; a square. That’s why $x^2$ is the area of a square in square units.

This is my explanation for the distributive property geometric interpretation:

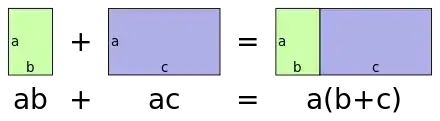
Here, we add a rectangle with area $a \times b$ with a rectangle with area $a \times c$ which I have explained in (1). Now, we can clearly see how this corresponds to adding the lengths and multiplying by the breadth.

From an algebraic standpoint, the only thing the distributive property really is is factoring out the $a$ in $ab + ac$.

The distributive property also works for any number of terms:

$a(b_1 + b_2 + \cdots + b_n) = ab_1 + ab_2 + \cdots + ab_n$

Hope this clears up confusion. If you have any more confusion, you can comment and I will edit this answer as per that.

---

I forgot to address fractions multiplication!

However, nothing changes with the area of a rectangle formula when you switch to fractions:

$A = lb$

And if you’d say $l$ and $b$ are fractions you would just get

$A = \frac{a}{b}\frac{c}{d}$

And, we know that multiplying fractions is just multiplying the numerators and denominators, so we get;

$A = \frac{ac}{bd}$

One of the most important things to note in Arithmeric and algebra is this:

Formulas don’t change when you plug in different things for the placeholders.

Hope this clears up confusion related to fraction multiplication.

Answer 2

As stated in the commentaries(see here), it is out of the question to prove conclusively that $$\forall x,y,z \in \mathbb R,x(y+z)=xy+xz$$On the other hand, one can easily answer by using the interpretation of xy as the area of a rectangle of sides $x$ and $y$ for $x,y>0$. This, however, seems to be OP's problem.

So let's recall the different drawings starting from the integers gradually to the reals :

First, we have to draw a square unit; then we can represent any integer, for example $2$ or $3$; then recall that the multiplication of integers can be interpreted, visualized as an area, for example $2\times 3=6$; Then the rationals are constructed to extend the properties of the integers. Let's take it easy by starting with the fractions of numerator 1. We have $$\frac13\times 2=\frac23$$ then for example $$\frac{7}{15}\times \frac13=\frac {7}{3\times15}$$ and finally $$\frac{7}{15}\times \frac23=\frac {2\times7}{3\times15}$$

Hence the natural definition of multiplying fractions by $$\forall a,b,c,d \in \mathbb Z\times \mathbb Z \times \mathbb Z^*\times \mathbb Z^*, \frac ac \times \frac bd:=\frac{ab}{cd}$$ which corresponds well to the interpretation in terms of area by construction in accordance with our intuition. That's why it makes sense.

Then, it's more complicated for reals: they are constructed, for example as sequences of rationals that are closer and closer. So we approach all real by a rational by construction, as close as we want and finally the interpretation of $xy$ as the desired area.

And the drawings from wikipedia for example.