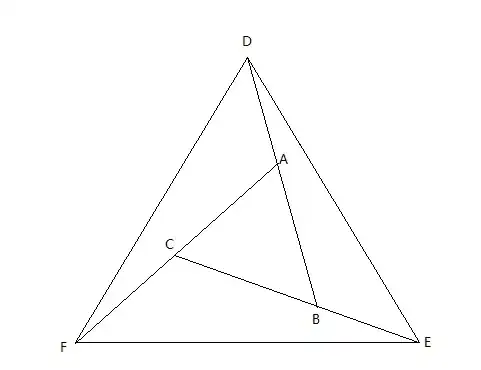
In the figure, AD=BE=CF. Moreover, DEF is an equilateral triangle. Must ABC be equilateral?

In the figure, AD=BE=CF. Moreover, DEF is an equilateral triangle. Must ABC be equilateral?
Yes, suppose that $\angle A$ is the largest angle of $\triangle ABC$, then $BC$ is the max side. Thus $$CE=\max(CE,FA,BD).$$ That is $$\angle CFE=\max(\angle ADF,\angle CFE,\angle BED).$$ or $$\angle CFD=\min(\angle CFD,\angle BDE,\angle CEF).$$
It follows that in $\triangle ABC$, $$\angle A=\angle ADF+\angle CFD\leq \angle CFE+\angle CEF=\angle C,$$ or $\angle A=\angle C$.
A ≤ C (not A = C). But you can easily extend A ≤ C by symmetry to A = B = C.
– M.M
Sep 08 '14 at 04:43
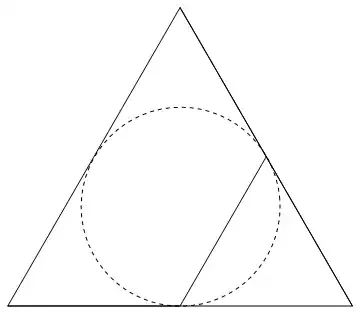
Not if DAB etc are not colinear. Consider the following:
However, if they are, the centre two triangles in this give a visual proof:
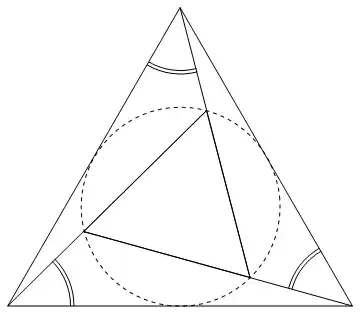
(added as visual complement to Quang Hoang's answer above)