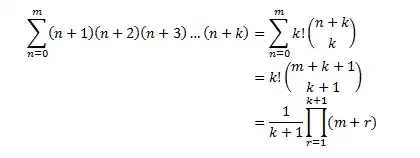Telescoping series of form $\sum (n+1)\cdots(n+k)$

Question

Wolfram Alpha is able to telescope sums of the form $\sum (n+1)\cdots(n+k)$

e.g. $(1\cdot2\cdot3) + (2\cdot3\cdot4) + \cdots + n(n+1)(n+2)$

How does it do it?

EDIT: We can rewrite as: $\sum {(n+k)! \over n!} = \sum k!{(n+k)!\over n!k!} = \sum k!{{n+k} \choose n}$ (Thanks Daniel Fischer)

EDIT2: We can also multiply out and split sums. So e.g.

$$\sum (n-1)n(n+1) = \sum (n^3-n) = \sum n^3 - \sum n$$

But sums of powers actually seem to be more nasty than the original question, involving Bernoulli numbers. (Thanks Claude Leibovici)

And is there any name for this particular corner of maths? (i.e. How might I go about searching the Internet for information regarding this?)

PS please could we have a 'telescoping' tag?

Answer 1

Hint: $$ \sum_{n=k}^m\binom{n}{k}=\binom{m+1}{k+1} $$ A generalization is discussed in this answer. The equation above is equation $(1)$ with $m=0$.

---

Telescoping sum

To turn the sum in the question into a "telescoping sum", we can use the recurrence for Pascal's Triangle: $$ \binom{n+1}{k+1}=\binom{n}{k}+\binom{n}{k+1} $$ Using this recurrence, we get $$ \begin{align} \sum_{n=k}^m\binom{n}{k} &=\sum_{n=k}^m\left[\binom{n+1}{k+1}-\binom{n}{k+1}\right]\\ &=\sum_{n=k+1}^{m+1}\binom{n}{k+1}-\sum_{n=k}^m\binom{n}{k+1}\\ &=\left[\binom{m+1}{k+1}+\color{#C00000}{\sum_{n=k+1}^m\binom{n}{k+1}}\right]-\left[\binom{k}{k+1}+\color{#C00000}{\sum_{n=k+1}^m\binom{n}{k+1}}\right]\\ &=\binom{m+1}{k+1}-\binom{k}{k+1}\\ &=\binom{m+1}{k+1} \end{align} $$ The sums in red are the terms that are telescoped out, leaving just the first and last terms. In this case, the last term $\binom{k}{k+1}=0$.

Answer 2

Let $$p_n=\prod_{r=1}^k (n+r)=\overbrace{(n+1)(n+2)\cdots(n+k)}^{k \ \text{terms}}$$ which is the product of $k$ consecutive integers.

Consider the difference of two consecutive terms, where each term is the product of $k+1$ consecutive integers, i.e. $$\begin{align} &\prod_{r=1}^{k+1}(n+r)-\prod_{r=0}^k(n+r)\\ &=\overbrace{\underbrace{(n+1)(n+2)\cdots(n+k)}_{p_n}(n+k+1)}^{(k+1) \ \text{terms}}-\overbrace{n\underbrace{(n+1)(n+2)\cdots(n+k)}_{p_n}}^{(k+1) \ \text{terms}}\\ &=p_n[(n+k+1)-n]\\ &=p_n(1+k) \end{align}$$

Hence, $$p_n=\prod_{r=1}^k (n+r)=\frac1{1+k}\left[\prod_{r=1}^{k+1} (n+r)-\prod_{r=0}^k (n+r) \right]$$ which is convenient for telescoping.

Required summation, $$\begin{align} S=\sum_{n=0}^{m}p_n&=\sum_{n=0}^{m} \prod_{r=1}^{k} (n+r)=\sum_{n=0}^{m}(n+1)(n+2)(n+3)\cdots (n+k)\\ &=\frac1{k+1}\sum_{n=0}^{m} \left[ \prod_{r=1}^{k+1} (n+r)-\prod_{r=0}^{k} (n+r)\right]\\ &=\frac1{k+1}\prod_{r=1}^{k+1} (m+r) \qquad \blacksquare\end{align}$$ by telescoping.

In your example, $k=3$, hence the general term is

$$(n+1)(n+2)(n+3)=\frac14\left[(n+1)(n+2)(n+3)(n+4)-n(n+1)(n+2)(n+3)\right]$$

Hence, by telescoping from $n=0$ to $m$, $$\begin{align}S&=1\cdot2\cdot3+2\cdot3 \cdot 4+\cdots +(m+1)(m+2)(m+3)\\ &=\frac14(m+1)(m+2)(m+3)(m+4) \end{align}$$

---

NB: It is interesting to note that this result bears a striking resemblance to integration.

Compare the standard integral $$\int_0^m n^k dn=\frac{m^{k+1}}{k+1}$$ to the result of the summation above, which can also be stated as $$\sum_{n=0}^{m}n^{[k]}=\frac {m^{[k+1]}}{k+1}$$ where $n^{[k]}$ is my adjusted* Pochhammer symbol for rising factorials, defined as $$n^{[k]}=\prod_{r=1}^{k}(n+r)=(n+1)(n+2)(n+3)\cdots(n+k)$$

The actual Pochhammer symbol for rising factorials, $n^{(k)}$, starts from $n$ itself and not $n+1$, i.e. $$n^{(k)}=\prod_{r=1}^{k}(n+r-1)=n(n+1)(n+2)\cdots(n+k-1)$$

Answer 3

For completeness, a solution using the combinatorial/binomial approach, as initiated by RobJohn:

Answer 4

Let $p(n, k) =n(n+1)...(n+k-1) =\prod_{j=0}^{k-1} (n+j) $.

Then (writing each step in detail)

$\begin{array}\\ p(n+1, k)-p(n, k) &=\prod_{j=0}^{k-1} (n+1+j)-\prod_{j=0}^{k-1} (n+j)\\ &=\prod_{j=1}^{k} (n+j)-\prod_{j=0}^{k-1} (n+j)\\ &=(n+k)\prod_{j=1}^{k-1} (n+j)-n\prod_{j=1}^{k-1} (n+j)\\ &=((n+k)-n)\prod_{j=1}^{k-1} (n+j)\\ &=k\prod_{j=1}^{k-1} (n+j)\\ &=k\prod_{j=0}^{k-2} (n+1+j)\\ &=kp(n+1, k-1)\\ \end{array} $

or, putting $k+1$ for $k$ and $n$ for $n+1$, $p(n, k) =\frac{p(n, k+1)-p(n-1. k+1)}{k+1} $.

Therefore

$\begin{array}\\ \sum_{n=1}^M p(n, k) &=\sum_{n=1}^M \frac{p(n, k+1)-p(n-1. k-1)}{k+1}\\ &=\frac1{k+1}\sum_{n=1}^M (p(n, k+1)-p(n-1. k+1))\\ &=\frac1{k+1}(p(M, k+1)-p(0, k+1))\\ &=\frac{p(M, k+1)}{k+1}\\ \end{array} $

Answer 5

$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ \begin{align}&\color{#c00000}{\sum_{n = 0}^{m}\pars{n + 1}\ldots\pars{n + k}}= \sum_{n = 0}^{m}{\pars{n + k}! \over n!} =k!\sum_{n = 0}^{m}{n + k \choose k} =k!\sum_{n = 0}^{m}\oint_{\verts{z}\ =\ 1}{\pars{1 + z}^{n + k} \over z^{k + 1}} \,{\dd z \over 2\pi\ic} \\[3mm]&=k!\oint_{\verts{z}\ =\ 1}{\pars{1 + z}^{k} \over z^{k + 1}} \sum_{n = 0}^{m}\pars{1 + z}^{n}\,{\dd z \over 2\pi\ic} =k!\oint_{\verts{z}\ =\ 1}{\pars{1 + z}^{k} \over z^{k + 1}} {\pars{1 + z}^{m + 1} - 1 \over \pars{1 + z} - 1}\,{\dd z \over 2\pi\ic} \\[3mm]&=k!\bracks{\oint_{\verts{z}\ =\ 1} {\pars{1 + z}^{k + m + 1} \over z^{k + 2}}\,{\dd z \over 2\pi\ic} -\oint_{\verts{z}\ =\ 1}{\pars{1 + z}^{k} \over z^{k + 2}}}\,{\dd z \over 2\pi\ic} \\[3mm]&=k!\bracks{{k + m + 1 \choose k + 1} - {k \choose k + 1}} \end{align}

$$ \color{#66f}{\large\sum_{n = 0}^{m}\pars{n + 1}\ldots\pars{n + k} =k!\,{k + m + 1 \choose m}} $$

Answer 6

Also your terms can be re written as $$n(n+1)(n+2)=\dfrac{n(n+1)(n+2)(n+3)}{4}-\dfrac{(n-1)n(n+1)(n+2)}{4}.$$

Answer 7

Following from RobJohn's hint, this can be proved very simply by reverse-engineering the hockey-stick identity.

The blues sum to the red for any given 'hockey-stick'.

It is a straightforward proof by induction. For example, in the picture, 1+3+6+10+15 = 35, so 1+3+6+10+15 + 21 = 35+21 = 56

i.e. True(stick length k) => True(stick length k+1)

Induction can also be argued from the ${n \choose r}$ formula, but the above method avoids algebraic manipulation, working instead from the simple "each element is formed by summing its upper neighbours" definition of Pascal's Triangle.

But now we DO need some algebraic manipulation.

We write this hockey-stick identity as:

$${k+0 \choose k} + ... + {k+n \choose k} = {k+(n+1) \choose (k+1)} $$

(notice the hockey stick has been reflected)

$$ {(k+0)! \over {k!((k+0)-k)!}} + ... + {(k+n)! \over {k!((k+n)-k)!}} = {(k+(n+1))! \over {(k+1)!(((k+(n+1))-(k+1))!}}$$

$$ {(k+0)! \over 0!} + ... + {(k+n)! \over n!} = {1 \over {k+1}} \cdot {(k+(n+1))! \over n!}$$

So the original question turns out to be an emergent property of Pascal's Triangle, and I would hazard a guess that it is from this simple construct that the question originally arose.

However, this proof doesn't move forwards from start to finish in a sequence of intelligently chosen moves. It doesn't offer any insight into telescoping general sums, hence I am favouring hypergeometric's proof.

Answer 8

Induction

This question is actually a duplicate of: Finding a closed formula for $1\cdot2\cdot3\cdots k +\dots + n(n+1)(n+2)\cdots(k+n-1)$

But it is difficult to find duplicates when the question can only be expressed using maths symbols, and this question now acts as a more comprehensive resource.

One of the answers to that question is to manually construct formulae for the first few cases: $1+2+3+\dots+n$, $1\cdot2 +\dots + n\cdot(n+1)$, etc, notice a pattern and intuit a candidate formula, then prove this by induction.