1

In this question obviously the error of our "approximation" is $4-\pi=0.858...$ . I tried to reconstruct the false argument with $\tau=2\pi$, and the error in that case would be $8-\tau=1.716...$, which is obviously quite close to $\sqrt{3}$. Is there any particular reason why $8-\tau$ is quite close to $\sqrt{3}$? Or, equivalently, is there any particular reason why $4-\pi$ is quite close to $\frac{\sqrt{3}}{2}$? Is this just a coincidence?

Community
  • 1
user132181
  • 2,726
  • Whatever the reason is, it is no coincidence. The value of pi is fixed and a fundamental property of nature, no coincidence. – Asier Calbet Aug 19 '14 at 15:33
  • What does "close" mean? Answering this question will show you that your question has not much sens... E.g. I think $10^{999999999}$ is close to $(10^{999999999}+132)$ but then $\pi$ is even closer to $124$... – Surb Aug 19 '14 at 15:38
  • @Surb well, $4-\pi$ is a bit over 99.1% of $\frac{\sqrt{3}}{2}$. I'm looking for an "explanation" akin to this one. – user132181 Aug 19 '14 at 15:49
  • 1
    I suspect that it's related to the fact that $4-\pi$ is the area remaining when the unit disk is removed from the square of side-length $2$. That would imply that a quarter of $\sqrt{3}/2$ is a good approximation of the 'corner' area. – Semiclassical Aug 19 '14 at 15:53
  • Why? For the same reason $\gamma$ is so close to $\dfrac1{\sqrt3}$ ;-) – Lucian Aug 19 '14 at 15:59

2 Answers2

2

Here is one explanation, though I'm not convinced it's the best one. Note that $4\int_0^1(1-\sqrt{1-x^2})\,dx=4-\pi$ (geometrically, this corresponds to $4-\pi$ being the area left over when the unit disk is removed from a square of side-length $2$). We can expand the integrand as $\dfrac{1}{2}x^2+\dfrac{1}{8}x^4+O(x^4)$, giving the integral approximation

$$4\int_0^1(1-\sqrt{1-x^2})\,dx\approx 4\left[\frac{1}{4}+\frac{1}{32}\right]=1+\frac{1}{8}$$

At the same time, we can do a binomial approximation of $\sqrt{3}/2$ as

$$\frac{\sqrt{3}}{2}=\sqrt{1-\frac{1}{4}}\approx 1-\frac{1}{8}$$ If the second term were positive, then the approximation of the OP would be justified; as it is, it only approximates the approximation.

Semiclassical
  • 15,842
  • Isn't your integration estimate wrong (unless you're doing a second estimation that I'm missing - trapezoidal or the like?) That estimate is clearly a very rough one, since the estimate is $\gt 1$ but it's very easy to see (either computationally or geometrically) that the integral isn't. I would have expected an estimate of the form $4\left(\left.(\frac16x^3+\frac1{40}x^5)\right|^1_0\right)\approx\frac{23}{30}$... – Steven Stadnicki Aug 20 '14 at 15:16
  • @StevenStadnicki: No, it's nothing interesting like that: I just completely derped the calculation. Yours is the correct one. – Semiclassical Aug 20 '14 at 15:20
  • What I find odd is that my approximation is also rough (off by .1), but that adding just $\frac1{10}$ to it gives a very good approximation; it had me wondering if I'd dropped a factor of two somewhere, but I don't see it... – Steven Stadnicki Aug 20 '14 at 15:38
  • @StevenStadnicki: From the POV of my answer, it's all about finding clever estimates of the above integral. Doing a binomial expansion about $x=0$ is guaranteed to be pretty rough since it'll always underestimate the integral. But evidently the 'corner' areas ignored in that way have fairly nice estimates as well (e.g. $1/10$), though I don't see why. – Semiclassical Aug 20 '14 at 15:57
2

Demonstration without words (except for these):

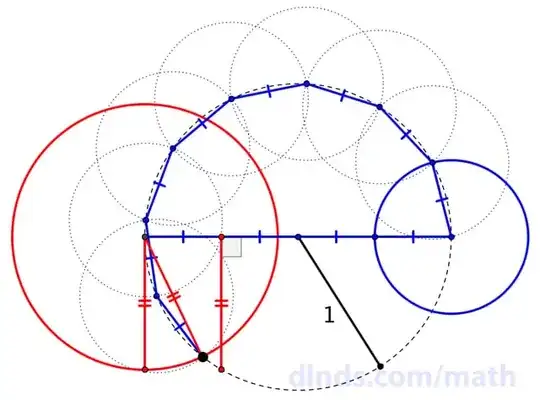
enter image description here

Blue
  • 75,673
  • 2
    I think I might need some words here. – syusim Aug 20 '14 at 16:36
  • 1
    @SamuelYusim: The blue polygonal arc has $8$ chords of length $1/2$; the big circular arc joining its endpoints therefore has length approximately $4$. That circular arc is clearly a semicircle, plus a smaller arc that's very-nearly subtended by the red chord of length $\sqrt{3}/2$; therefore, the big arc has length also approximated by $\pi + \sqrt{3}/2$. This gives $4 \approx \pi + \sqrt{3}/2$, as desired. – Blue Aug 20 '14 at 17:49
  • 1
    @SamuelYusim: Of course, the approximations are varying degrees of bad here, so the diagram hardly constitutes a rigorous numerical argument. A more-refined diagram would have blue and red chords hugging the circle more-closely. Even so, it's rather striking that the blue and red chords seem to meet so well at this very rough stage. – Blue Aug 20 '14 at 17:50