How far can one see over the ocean?

Question

Since Earth is a sphere, one has only a limited visibility radius. How far is that, actually?

This Q&A was inspired by this question, about whether or not Legolas can see the 24km distant Riders of Rohan.

Answer 1

I have up-voted the answer by M.Herzkamp, but I also think he makes it somewhat more complicated than it needs to be. The distance from the center of the earth to your eye is $r+h$, where $r$ is the radius of the earth and $h$ is the height of your eye above the ground. The distance from the center of the earth to a point on the horizon is $r$. The distance from your eye to the point on the horizon let us call $d$. The three sides of a right triangle are then the legs, $r$ and $d$, and the hypotenuse $r+h$. Applying the Pythagorean theorem, we have $$ r^2 + d^2 = (r+h)^2. $$ It follows that $$ d^2 = (r+h)^2 - r^2 $$ so $$ d=\sqrt{(r+h)^2-r^2}. $$ This admits simplifiction: $$ d=\sqrt{(r+h)^2-r^2} = \sqrt{(r^2+2rh+h^2) - r^2} = \sqrt{2rh + h^2}. $$ When $h$ is tiny compared to $r$, we can say $$ d \approx \sqrt{2rh\,{}}. $$

Answer 2

Let us suppose, an observer of height $h$ stands on a perfectly spherical planet of radius $r$:

Edit: here is an easier way, making use of the right angle between the line of sight and the radial ray. You can just use the definition of the cosine:

$$ \cos(\theta_T) = \frac{r}{r+h} \qquad \Rightarrow \qquad s = r\cdot\theta_T = r\cdot\cos^{-1}\!\!\left(\frac{r}{r+h}\right) $$

which is equivalent to the solution obtained by the complicated method. /Edit

The distance $s$ to the farthest point he can then see is determined by the tangent to the semi circle through his head. If you describe the semi circle in a cartesian coordinate system by $$ y^2+x^2 = r^2, $$ the observer's head is at $y=r+h,\ x=0$.

To obtain the slope of the tangent, we plug the tangent equation $y=mx+r+h$ into the circle equation and solve for $x$: $$ x_{1/2} = -(r+h)\frac{m}{1+m^2} \pm \sqrt{\frac{(r+h)^2m^2}{(1+m^2)^2}+\frac{r^2-b^2}{1+m^2}} $$ Those are two intersection points, and in order to have a tangent, they must be equal. That is the case, if the term under the square root is zero. The resulting equation can be solved for $m$: $$ m_{\pm} = \pm \sqrt{\frac{(r+h)^2}{r^2}-1} $$ Let's take the negative solution for the tangent on the right (it does not matter), and calculate the tangent point: $$ x_T = -(r+h)\frac{m_-}{1+m^2_-} = \frac{r}{r+h}\sqrt{(r+h)^2-r^2} $$ The viewing distance angle is $\theta_T = \text{asin}(x_T)$. To get the viewing distance, we observe that $$ \frac{s}{2\pi r} = \frac{\theta_T}{\text{full angle}} = \frac{\theta_T}{2\pi}\text{, with angle in radian} $$ $$ \Rightarrow s(h) = r\cdot\text{asin}\left(\sqrt{1-\frac{r^2}{(r+h)^2}}\right) $$ If you plot this for $h$ small compared to $r$, it resembles a square root function, and indeed, $$ \lim_{h\rightarrow0^+}\frac{s(h)}{\sqrt{h}} = \sqrt{2r} $$ which means that for small heights, the viewing distance can be described as $$ s(h) \approx \sqrt{2rh} $$ On Earth ($r\approx6371\text{km}$), a normal person ($h\approx1.8\text{m}$) can see the surface about 4.8km away. Not much further. If you climb a hill or tree ($h\approx 50\text{m}$), your range increases to 25km!

Answer 3

Atmospheric refraction cannot be neglected. As mentioned here the effect of this can be taken into account approximately by pretending as if the Earth's radius is larger by a factor of 7/6. This makes the distance $d$ to the horizon when the height $h$ is much less than the Earth's radius $R$ equal to

$$d = \sqrt{\frac{7}{3} R h}$$

Answer 4

If you go sailing, you'll have about 5 nautical miles of visibility (1nm = 1852m). I personally find the nomogram a delightful invention:

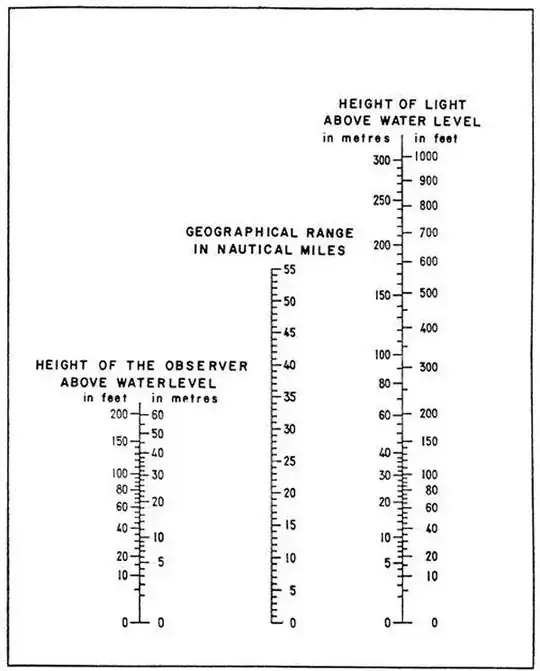
Simply draw a straight line between the height of the observer and the height of the object on the horizon (in this case = 0), then read off the geographical range.