Finding the Distance to the Horizon

Question

The question is as follows:

Flying at an altitude of 39000 feet one clear day, Cameron looked out the window of the airplane and wondered how far it was to the horizon. Rounding your answer to the nearest mile, answer Cameron’s question.

There was a previous problem that stated that we should assume that Earth's radius has a 3,960-mile radius, and, after conversion, I got the radius (in feet) to be 20,908,800 feet. I don't know how to go further from there. Any help will be greatly appreciated!

try drawing a circle, and from the circle a point above. Now draw the tangent from to the point to the circle, and you should find yourself with some trignometry to play about with :) — mdave16, Oct 15 '17 at 02:19
@mdave16 You don't even really need trig---just the Pythagorean theorem. — Xander Henderson, Oct 15 '17 at 02:22
Also, this appears to be a duplicate of this question. Michael Hardy gives a nice answer, and a good argument for making approximations that disregard the altitude squared term (which, for altitudes that are a couple of orders of magnitude less than the radius of the Earth, gives good results). — Xander Henderson, Oct 15 '17 at 02:53
Is it just me who thinks that the most error-prone part is the unit conversion? — Hagen von Eitzen, Oct 15 '17 at 11:46

score 7 · Accepted Answer · answered Oct 15 '17 at 02:31

7

Hint: Consider the illustration:

answered Oct 15 '17 at 02:31

robjohn

345,667

Thank you so much for this diagram! It helped me so much! I just have a quick question- Why does the point where Cameron is looking from to the horizon tangent to one another? – geo_freak Oct 15 '17 at 02:39
3

@geo_freak It's a rule of circles that the radius is always perpendicular to the tangent, and the horizon is where your line of sight is tangent to the earth – D.R. Oct 15 '17 at 02:42
Got it. Thank you @D.R. – geo_freak Oct 15 '17 at 02:43

score 5 · Answer 2 · edited Oct 15 '17 at 12:20

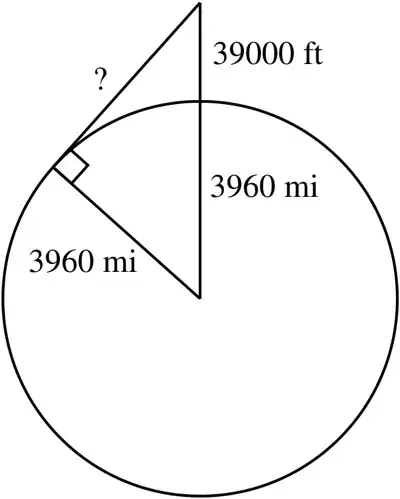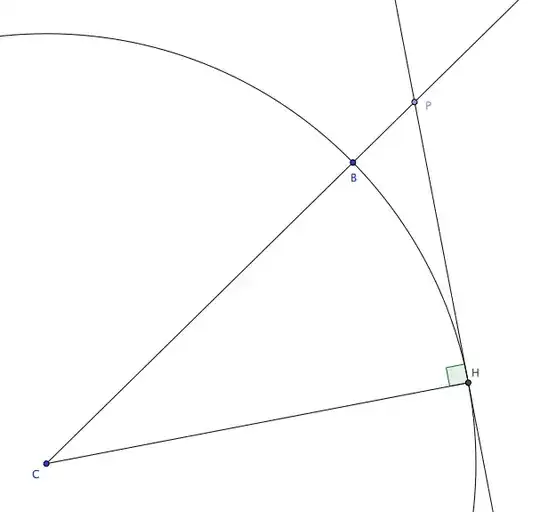
In the picture, $P$ is the plane, $C$ is the center of the Earth, $B$ is the point on the surface of the Earth directly below the plane, and $H$ is (a point on) the horizon. Our goal is to find $\ell(PH)$, i.e. the length of $PH$, i.e. the distance form the plane to the horizon.

Note that the line $\overline{PH}$ must be tangent to the surface of the Earth: a point on the horizon is the farthest point that can be seen from a given vantage point. If $\overline{PH}$ were not tangent to the surface of the Earth, then there would be another point on the Earth farther from the plane that could be seen from the plane, which is a contradiction.

Since the line $\overline{PH}$ is tangent to the surface of the Earth, we know that $\angle CHP$ is a right angle (radii and tangents passing through the same point on a circle are always perpendicular; this takes a little bit of proving, but essentially follows from a clever application of the Pythagorean theorem). Moreover, we know the lengths of the segments $CB$ and $CH$ (these are radii of the Earth), and $BP$ (this is the altitude of the plane. Therefore, as $\triangle CHP$ is a right triangle, we can apply the Pythagorean theorem to get \begin{align} \ell(CH)^2 + \ell(PH)^2 = \ell(CP)^2 &\implies (3960\text{ miles})^2 + (x)^2 = (3960\text{ miles} + 39000\text{ ft})^2 \\ &\implies x = \sqrt{(3960\text{ miles} + 39000\text{ ft})^2 - (3960\text{ miles})^2}. \end{align} Since there are 5280 feet in every mile, we can convert feet to miles via the computation $$ 39000\text{ ft} = 39000\text{ ft} \cdot\frac{1\text{ mile}}{5280\text{ ft}} \approx 7.386\text{ miles}.$$ Plugging this back into the previous equation (and simplifying the units a bit), we finally get \begin{align} x &\approx \sqrt{ (3960 + 7.386)^2 - (3960)^2 }\text{ miles} \\ &\approx \sqrt{ 2(3960)(7.386) + (7.386)^2} \text{ miles} \\ &\approx \sqrt{ 58497.12 - 54.55 } \text{ miles} \\ &\approx 242 \text{ miles}. \end{align}

Finding the Distance to the Horizon

2 Answers2