Hoping to get some help with the following problem
Given that $w = e^{(2\pi/5)i}$, show that $w + \overline{w}$ is a root of $z^2 + z - 1 = 0$.
I've noticed that $w + \overline{w} = 2Re(w)$, but I'm not sure on how to proceed from there. $2\pi/5$ is a weird angle, so substituting a cosine doesn't seem to make much sense.
Note that $w^4 = \overline{w}$, $w^3 = \overline{w^2} = \overline{w}^2$.
We have $1+w+w^2+w^3+w^4 = {1-w^5 \over 1 -w} = 0$.
That is, $1 + (w + \overline{w}) + (w^2 + \overline{w}^2) = 1 + (w + \overline{w}) + (w + \overline{w})^2 -2 = (w + \overline{w})^2 + (w + \overline{w}) -1 = 0$.
$w + \overline{w} = 2\cos (2\pi/5)$, and $(2\cos (2\pi/5))^2 + 2\cos (2\pi/5) - 1 = 4\left(\dfrac{1+\cos (4\pi/5)}{2}\right) + 2\left(2\cos^2(\pi/5) - 1\right) - 1 = 2\left(1-\cos (\pi/5)\right) + 4\cos^2(\pi/5) - 2 - 1 = 4\cos^2(\pi/5) - 2\cos (\pi/5) - 1 = S$.
We have: $\cos 36^\circ = \sin 54^\circ$ gives: $1-2x^2 = 3x - 4x^3$ with $x = \sin 18^\circ = \sin (\pi/10)$. Thus: $4x^3 - 2x^2 - 3x + 1 = 0 \to (x-1)(4x^2 + 2x - 1) = 0$. Since $0 < x < 1$, $4x^2 + 2x - 1 = 0$. Thus : $\cos (\pi/5) = 1 - 2x^2 = 1 - \dfrac{1-2x}{2} = \dfrac{1+2x}{2}$, and $\cos^2(\pi/5) = \left(\dfrac{1+2x}{2}\right)^2 = \dfrac{1+4x+4x^2}{4} = \dfrac{1+4x+1-2x}{4} = \dfrac{1+x}{2}$. Thus: $S = 4\left(\dfrac{1+x}{2}\right) - 2\left(\dfrac{1+2x}{2}\right) - 1 = 0$.
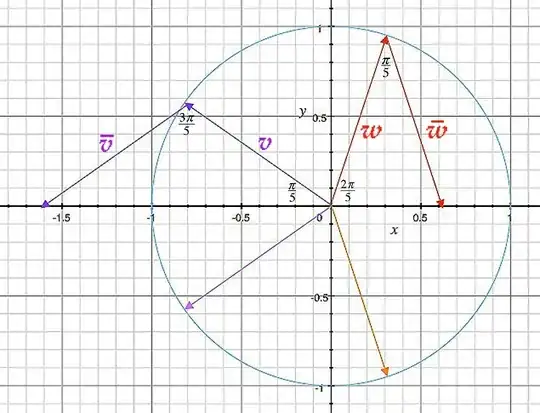
We may treat $ \ w \ = \ e^{i·2\pi/5} \ $ and $ \ \overline{w} \ = \ e^{-i·2\pi/5} \ $ as unit vectors in the complex plane, as seen in the graph above. Placing them head-to-tail, they then form two sides of an isosceles triangle in which their vector sum $ \ w + \overline{w} \ $ is the third side lying in the real-axis. We shall call the length of that side $ \ z_1 \ \ ; $ as the apex angle of this triangle has measure $ \ \pi/5 \ \ , $ we have $ z_1^2 \ = \ 1^2 + 1^2 - 2·1·1·\cos \frac{\pi}{5} \ = \ 2·(1 - \cos \frac{\pi}{5} )\ \ . $
If we employ the cosine-squared identity, we may also write $$ \ \left(\cos \frac{2\pi}{5} \right)^2 \ = \ \frac12 · \left(1 \ + \ \cos \frac{4\pi}{5} \right) \ \ \Rightarrow \ \ \left(2 · \cos \frac{2\pi}{5} \right)^2 \ = \ 2 · \left(1 \ + \ \cos \frac{4\pi}{5} \right) \ \ , $$ and, since $ \ \cos \frac{4\pi}{5} = -\cos \frac{\pi}{5} \ \ , $ $$ \left(2 · \cos \frac{2\pi}{5} \right)^2 \ = \ 2 · \left(1 \ - \ \cos \frac{\pi}{5} \right) \ = \ z_1^2 \ \ . $$ (We also see this in that $ \ \cos \frac{2\pi}{5} \ $ is one-half of the base of the isosceles triangle.)
We can find the trigonometric values of interest from dissection of a unit regular pentagon (as mentioned on this site going back to here). By drawing in two diagonals of the pentagon, which has interior angles $ \ \frac{3\pi}{5} \ \ , $ we form a unit parallelogram and two sets of similar triangles.
The isosceles triangle we have been discussing appears here, for instance, as $ \ \Delta ABF \ \ , $ with unit sides and base $ \ x \ \ . $ The other type of isosceles triangle is represented by $ \ \Delta ABC \sim \Delta CFB \ \ . $ Between those triangles, we can set up the proportionality $$ \frac{x}{1} \ = \ \frac{1}{1 \ + \ x} \ \ \Rightarrow \ \ x·(1 \ + \ x) \ = \ 1 \ \ \rightarrow \ \ z^2 \ + \ z \ - \ 1 \ \ = \ \ 0 \ \ , $$ which is the equation for which we are seeking roots. So one of these is $ \ z_1 \ = \ 2 · \cos \frac{2\pi}{5} \ \ . $
We have demonstrated the proposition of the problem, but we can say rather more. A basic relation for the "golden ratio" $ \ \phi \ $ (some people prefer $ \ \tau \ $) is $ \ \frac{1}{\phi} + 1 \ = \ \phi \ \ ; $ returning to $ \ x·(1 \ + \ x) \ = \ 1 \ \ , $ we find $ \ \frac{1}{\phi}·\left(1 \ + \ \frac{1}{\phi} \right) \ = \ \frac{1}{\phi}·\phi \ = 1 \ \ . $ Applying the quadratic formula to $ \ z^2 + z - 1 \ = \ 0 \ \ , $ we obtain $ \ x \ = \ \frac{-1 \ \pm \ \sqrt5}{2} \ \ . $ The positive root of the quadratic equation then tells us that $$ z_1 \ \ = \ \ 2 · \cos \frac{2\pi}{5} \ \ = \ \ \frac{1}{\phi} \ \ = \ \ \frac{-1 \ + \ \sqrt5}{2} \ \ \approx \ \ 0.61803 \ \ . $$
The other root of this quadratic equation is also contained in the golden-ratio relation:
$$ \frac{1}{\phi} + 1 \ = \ \phi \ \ \Rightarrow \ \ 1 - \phi \ = \ -\frac{1}{\phi} \ \ ; $$ $$ x·(1 \ + \ x) \ = \ 1 \ \ , \ \ \text{so} \ -\phi·(1 \ - \ \phi ) \ = \ -\phi·\left(-\frac{1}{\phi} \right) \ = 1 \ \ . $$
This corresponds to the unit vector sum $ \ v + \overline{v} \ \ , $ with $ \ v \ = \ e^{i·4\pi/5} \ \ , $ in the graph at the top and $ \ \Delta ABC \ $ in the pentagon diagram. The second root is then $$ z_2 \ \ = \ \ 2 · \cos \frac{4\pi}{5} \ \ = \ \ -\phi \ \ = \ \ \frac{-1 \ - \ \sqrt5}{2} \ \ \approx \ \ -1.61803 \ \ . $$
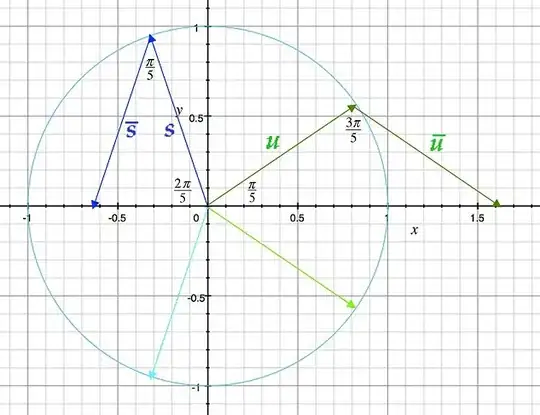
By similar reasoning, we can also find the roots of $ \ z^2 \ - \ z \ - \ 1 \ = \ 0 \ \ . $ Writing $ \ z·(z \ - \ 1) \ = \ 1 \ $ and the golden-ratio relation as $ \ \phi - 1 \ = \ \frac{1}{\phi} \ \ , $ we obtain $$ u \ = \ e^{i·\pi/5} \ \ \rightarrow \ \ z'_1 \ \ = \ \ 2 · \cos \frac{\pi}{5} \ \ = \ \ \phi \ \ = \ \ \frac{+1 \ + \ \sqrt5}{2} \ \ $$ and $$ s \ = \ e^{i·3\pi/5} \ \ \rightarrow \ \ z'_2 \ \ = \ \ 2 · \cos \frac{3\pi}{5} \ \ = \ \ -\frac{1}{\phi} \ \ = \ \ \frac{+1 \ - \ \sqrt5}{2} \ \ , $$ as depicted in the graph below.
