Intuitive ways to get formula of cubic sum

Question

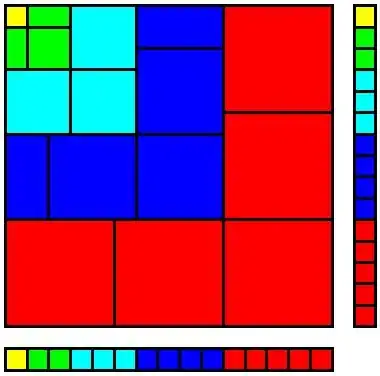
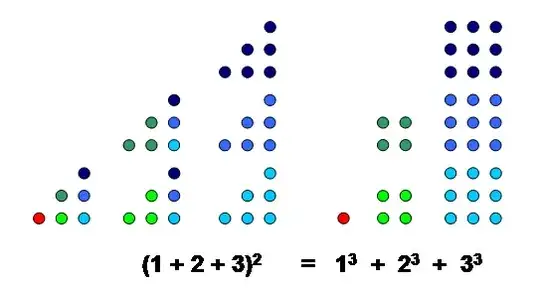Is there an intuitive way to get cubic sum? From this post: combination of quadratic and cubic series and Wikipedia: Faulhaber formula, I get $$1^3 + 2^3 + \dots + n^3 = \frac{n^2(n+1)^2}{4}$$ I think the cubic sum is squaring the arithmetic sum $$1^3 + 2^3 + \dots + n^3 = (1 + 2 + \dots + n)^2$$ But how to prove it? Please help me. Grazie!

Answer 1

We have $$ \sum_{k=1}^{n}k^3 = 1 + 8 + 27 + \ldots + n^3 = \\ \underbrace{1}_{1^3} + \underbrace{3+5}_{2^3} + \underbrace{7 + 9 + 11}_{3^3} + \underbrace{13 + 15 + 17 + 19}_{4^3} + \ldots = \\ \underbrace{\underbrace{\underbrace{1}_{1^2} + 3}_{2^2} + 5}_{3^2} + \ldots $$ which is $$ \left( \sum_{k=1}^{n}k \right)^2 $$

Answer 2

Maybe this will help you visualize it:

Source.

or this one which is clearer:

$\phantom{XXXXXXXX}$

Answer 3

Here are some 'Proof without Words' for this identity;

As Hakim showed (but this one might be slightly clearer);

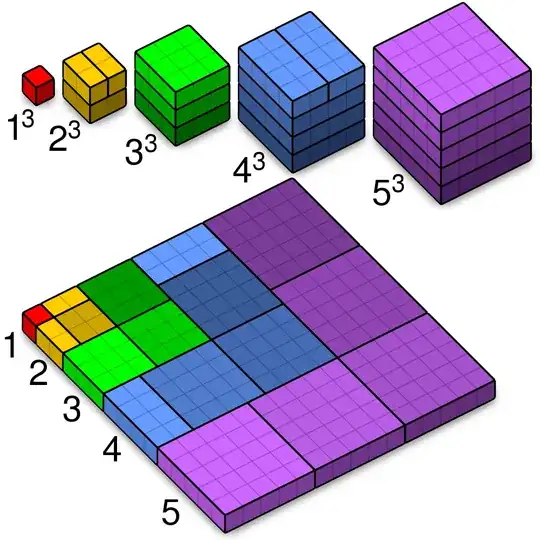
Here's another very clean illustration by Anders Kaseorg;

Here, the total top volume is undoubtedly $1^2+2^2+3^3+\cdots +n^2,$ while on the volume of the bottom part is; $$1\left(1+2+\cdots+n\right)+2\left(1+2+\cdots+n\right)+\cdots +n\left(1+2+\cdots+n\right)=\left(1+2+\cdots+n\right)^2.$$

Answer 4

Here's a proof by induction I came up with about two years ago.

Let $s_k(n) =\sum_{i=1}^n i^k $. Want to show that $s_3(n) = (s_1(n))^2 $.

If you want to prove by induction that $a(n) = b(n)$, there are two possibilities: (1) Show $a(0)-b(0) = 0$ and $a(n)-b(n) = 0 \implies a(n+1)-b(n+1) = 0$; (2) show $a(0) = b(0)$ and $a(n) = b(n) \implies a(n+1)-a(n) =b(n+1)-b(n) $.

These are, of course, equivalent, but I find that (2) is often easier since the math is simpler in the initial parts.

In this case, $s_3(n+1)-s_3(n) =(n+1)^3 =n^3+3n^2+3n+1 $ and

$(s_1(n+1))^2-(s_1(n))^2 =(s_1(n)+n+1)^2-(s_1(n))^2\\ =s_1^2(n)+2(n+1)s_1(n)+(n+1))^2-(s_1(n))^2\\ =2(n+1)s_1(n)+n^2+2n+1\\ $

so we want to show that $n^3+3n^2+3n+1 =2(n+1)s_1(n)+n^2+2n+1 $ or $n^3+2n^2+n =2(n+1)s_1(n) $ or $n(n^2+2n+1) =2(n+1)s_1(n) $ or $n(n+1)^2 =2(n+1)s_1(n) $ or $s_1(n) =\dfrac{n(n+1)}{2} $.

This can either be assumed known or, in turn, proved by induction using $\dfrac{(n+1)(n+2)}{2} -\dfrac{n(n+1)}{2} =\dfrac{n^2+3n+2-(n^2+n)}{2} =\dfrac{2n+2}{2} =n+1 $.