2

In linear algebra rotations are represented by matrices, i.e. linear transformations

How do you formally prove that rotation is a linear transformation?

But this page is very interesting

http://www.euclideanspace.com/maths/geometry/rotations/theory/

it vaguely talks about rotations as being quadratic in the way that the length of a vector is quadratic

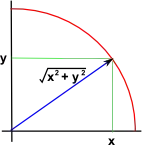
enter image description here

then it also shows how a rotation takes in something quadratic and spits out something linear

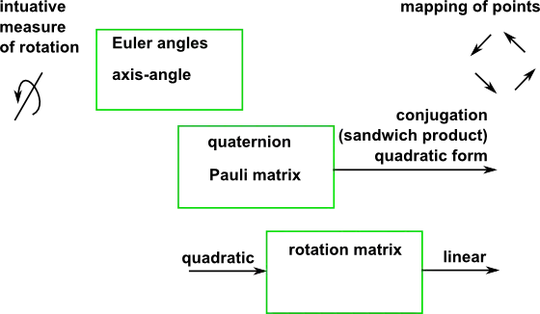
enter image description here

but it also vaguely hints that the 'quadratic-ness' as being encoded in rotating your basis vectors

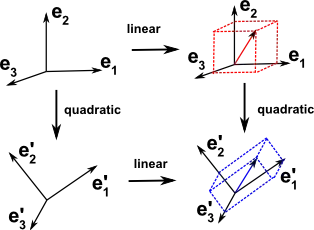
enter image description here

Is there a way to make all this precise with rigorous linear operators, bilinear and quadratic forms etc...?

It's very hand-wavey, but cool if correct.

I'm guessing this 'quadratic' business means tensors, bilinear forms etc... so I guess they're saying that all the rotation matrices, unitary geometry etc... is properly thought of as part of bilinear algebra rather than linear algebra - make sense?

Community
  • 1
bobby
  • 689
  • 2
    A linear transformation $A$ satisfies $A(\vec{x}+\vec{y}) = A(\vec{x}) + A(\vec{x}y)$ and $A(a\vec{x}) = a A(\vec{x})$... – johannesvalks Jul 16 '14 at 20:35
  • To me this so-called "quadraticness" is just related to the fact that the rotation matrix has complex eigenvalues. There's a nice book on the topic from Simon Altmann called Rotations, Quaternions and Double Groups. – citronrose Jul 16 '14 at 20:44
  • Someone doesn't know how to spell "intuitive". – Michael Hardy Jul 16 '14 at 21:34

1 Answers1

2

A rotation satisfies $A(x+y)=A(x)+A(y)$ and $A(ax)=aA(x)$, therefore it is a linear transformation (shamelessly stolen from johannesvalks).

Furthermore, the length of a vector is not "quadratic". There's a square root in there that makes it non-quadratic. It's only the square of the length of a vector that is quadratic, but that's not what we're talking about.

Klaas van Aarsen
  • 5,908