11

What is a differential? And how is it useful? What is its practical use?

For example, in Electromagnetic Wave Theory as it pertains to diffraction gratings, we have an equation like this one: $$d_s\sin(\theta) = m\lambda.$$

(Not important, but in case you're curious: $d_s$ is the distance between slits in the grating, $\theta$ is an approximate angle at which light bends through each slit of the grating, $\lambda$ is the wavelength of the light passing through the gradient, and $m$ is the number of wavelengths by which distances traveled by one ray from one slit differ from an adjacent slit.)

My physics book says that the differential of the above mentioned equation is $$d_s \cos(\theta)d\theta = md\lambda$$ (without confusing the single $d_s$ (distance) with the ones in $d\theta$ and $d\lambda$).

What does this mean and how is it useful? I am trying to understand the concept behind the differentials more so than the physics so that I may later make sense of the physics.

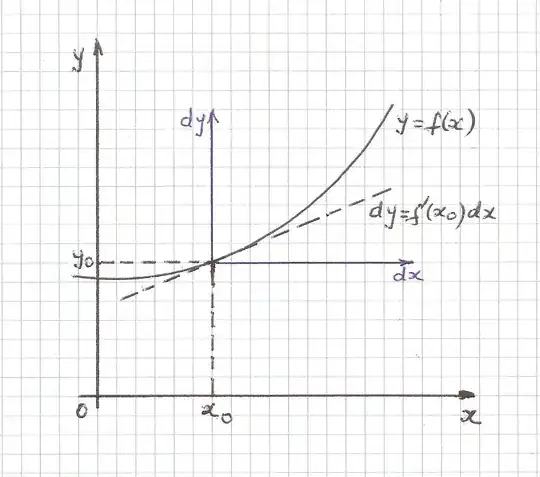
EDIT: In user6786's question, user6786 states that "according to the formula $dy=f'(x)dx$ we are able to plug in values for $dx$ and calculate a $dy$ (differential)". I'm trying to see how that works.

Community
  • 1
trusktr
  • 275
  • I've added LaTeX formatting to your question. By the way, if you see a piece of LaTeX you want to know the code for on the site, you can right click on it and choose "Show Source" - this is a good way of picking up how to do things. – Zev Chonoles Nov 28 '11 at 03:00
  • By the way - would you prefer it if I replace $X$ with $\theta$ and $A$ with $\lambda$? – Zev Chonoles Nov 28 '11 at 03:01
  • Aha, I see how to do it in the source. Pretty nice. – trusktr Nov 28 '11 at 03:03
  • 1
    +1. Using $d$ as a variable in a post about differentials makes it a bit hard to read (e.g., look at the expression $d \cos \theta d \theta$). Is it ok if we change that to $D$ instead? – Srivatsan Nov 28 '11 at 03:11
  • Sure. I also had fixed a typo: the first equation uses $\sin$, not $\cos$. – trusktr Nov 28 '11 at 03:14
  • 2
    See this, this, and this for related questions. – Arturo Magidin Nov 28 '11 at 03:14
  • 3
    @trusktr: I changed the $d$ of "distance between slits" to "$d_s$". Sufficiently close that it won't confuse you, sufficiently different that it won't confuse us. – Arturo Magidin Nov 28 '11 at 03:18
  • Those are nice answers Arturo. What are some practical ways to use differentials? – trusktr Nov 28 '11 at 05:12
  • 2
    Local linear approximations can be restated in terms of differentials: if $y=f(x)$, then $f(b)-f(a) = \Delta y \approx dy = f'(a)dx = f'(a)\Delta x$, which yields the "usual" formula, $f(b) \approx f(a) + f'(a)dx$. – Arturo Magidin Nov 28 '11 at 05:50
  • It's somewhat unfortunate, but differential approximation corresponds more directly to tangent vectors rather than to differentials. :( –  Nov 28 '11 at 06:05
  • Related material: MIT OCW Multivariable Calculus. In this course differentials are introduced and used. – Pratik Deoghare Nov 28 '11 at 06:23
  • Hmmmm... I guess perhaps I'm confused by the wording. I replaced "differential" with "derivative" and it makes much more sense: $d_s\cos\theta d\theta=md\lambda$ is the derivative of $d_s\sin\theta=m\lambda$. Now it makes perfect sense. The word "differential" was making me think of the integral for some reason. – trusktr Nov 28 '11 at 06:29
  • @trusktr: They are closely related, but they are not equal. – Arturo Magidin Nov 28 '11 at 17:44
  • I couldn't understand what they meant by the second equation being the differential of the first. It makes more sense to say that the second equation is the derivative of the first and can be used to find small differentials of the variables in the first equation. In this new light (better verbage by using "derivative" instead of "differential" to describe the second equation as it relates to the first), I'd rather just use the original equation for finding changes in the values since I already know what the original equation is and don't have to find any sort of anti-derivative. – trusktr Nov 29 '11 at 01:35
  • I see where using the derivative to determine small differentials might be be slightly inaccurate, but much easier in situations where determining the anti-derivative might be extremely complex. – trusktr Nov 29 '11 at 01:36
  • I honestly do not understand what trusktr means by "practical application"... – Mariano Suárez-Álvarez Apr 01 '12 at 18:44
  • @Arturo, maybe it's better to use $f'(a)dx \approx f'(a)\Delta x$ and $f(b) \approx f(a) + f'(a)\Delta x$. – Tom Copeland Apr 01 '12 at 22:47
  • @TomCopeland: Sorry... better for what? I don't seem to have participated in this post for over four months. – Arturo Magidin Apr 02 '12 at 00:20
  • @Arturo, your comment on local linear approximations prompted me to review the concept and notation, and after mulling over Loomis and Sternberg'S discussion and figure on pg. 141 of Advanced Calculus (revised edition), I now agree with your notation. – Tom Copeland Apr 03 '12 at 07:47

1 Answers1

6

EDIT to add: For the correct interpretation of your particular equations in terms of the Physics' content I advice you to ask it in the physics.SE site.

Let $y=f(x)$ be a real function. If $f(x)$ is differentiable for a particular value of $x_0$, then the the expression $$dy=f'(x_0)dx$$ is called the differential of $f$ at $x_0$. In the picture below this equation in $dx,dy$ represents the tangent line to the graph of $f(x)$ at $x_0$ in the translated coordinates system $dx,dy$. Both $dy$ and $dx$ are interpreted as infinitesimals. The differential $dy$ is approximately the change of $y$ when $x$ changes by an arbitrary small quantity $dx$. If $y=kx$, $dy$ is exactly equal to the change of $y=f(x)$.

enter image description here

  • Example: Consider the function $y=x^{2}$. The differential $dy$ at a generic point $x$ is $dy=2xdx$ and the finite difference $\Delta y$ is given by $$\begin{eqnarray*} \Delta y &=&(x+dx)^{2}-x^{2}=2xdx+(dx)^{2} \\&=&dy+(dx)^{2} \\ &\approx &dy,\end{eqnarray*}$$ if we neglect the contribution of $(dx)^{2}$. If we have a square, whose side length $x\approx 10 \;\mathrm{cm}$ was measured with a maximum error of $\pm 0.001 \mathrm{cm}$, its area can be computed approximately by the differential $$\begin{equation*} dy=2xdx=2\cdot 10\cdot 10^{-3}=0.02\;\mathrm{cm}^{2}. \end{equation*}$$ The error in this approximation is of the order of $$(dx)^{2}=\left( 10^{-3}\right) ^{2}=10^{-6} \;\mathrm{cm}^{2}.$$
  • If $f=u(x,y)$ is a function of the real variables $x,y$, then the first order differential form $du$ in two variables evaluated at $x_0,y_0$ is $$du=(\partial u/\partial x)|_{(x_0,y_0 )} \;dx+(\partial u/\partial y )|_{(x_0,y_0 )} \; dy.$$ And similarly for higher dimensions.
  • Differentials appear also in the transformation of integrals. Example: the area differential $dxdy$ becomes $rd\theta dr$, when we make a transformation from Cartesian to polar coordinates, and we have $$\iint \;dxdy=\iint \;r\;d\theta dr.$$ (See this question).

Concerning the equations my interpretation is as follows.

  1. For an arbitrary small change $d\theta $ of the angle $\theta $ there is a corresponding change $d\lambda $ of the wavelength $\lambda $, which means that $\lambda $ has to be a function of $\theta $. Otherwise $d\lambda =0$.

  2. If we differentiate each side of the equation $$\begin{equation*}d_{s}\sin \theta =m\lambda \end{equation*},$$ we get $$\begin{eqnarray*} \frac{d}{d\theta }\left( d_{s}\sin \theta \right) &=&\frac{d}{d\theta } m\lambda \\d_{s}\cos \theta &=&m\frac{d\lambda }{d\theta }, \end{eqnarray*}$$ which can be written in terms of differentials as $$ \begin{equation*}d_{s}\cos \theta \;d\theta =m\;d\lambda.\end{equation*}$$

Community
  • 1
Américo Tavares
  • 38,602