6

Hi I need help in understanding this:

if $\sin x = t$ then $\cos x dx = dt$.

My math book mostly uses the Lagrange's notation (prime) and I think I may not fully have grasped the $\frac{dx}{dy}$ way of writing and calculating the derivative of a function, since I am having a hard time to truely understand the statement above.

If anyone can give some explanation on how this logic works, I would be more than happy :)

Thank you!

Américo Tavares
  • 38,602
Lukas Arvidsson
  • 2,376
  • 1
    it seems that you are taking the derivative of $\sin x$ with respect to $x$, then multiplying both sides by $dx$ to clear the "denominator". See this: http://math.stackexchange.com/questions/21199/is-dy-dx-not-a-ratio/21209#21209 – Holdsworth88 Nov 11 '12 at 13:35
  • When you write $t=\sin(x)$ you are considering $t$ as a function of $x$, that is, $t(x)=\sin(x)$. So you can derivate $t$ with respect to $x$. Then $\frac{d}{dx}t(x)=\frac{d}{dx}\sin(x)=\cos(x)$. – Sigur Nov 11 '12 at 13:37

3 Answers3

4

$$t=\sin\ x \implies t+dt=\sin(x+ dx)=\sin x\cos dx+\cos x \sin dx$$

$$dx \approx 0\implies \sin dx \approx dx \ \text{ and } \ \ \cos dx \approx 1$$ Here the property ($ \sin x \approx x \text{ when } x\approx 0$) was applied, hence $\sin dx \approx dx$

$$t+dt=\sin x\cos dx+\cos x \sin dx = \sin x + \cos x \cdot dx$$ $$\text{$\sin x =t$ so $t+dt= t+ \cos x \cdot dx\implies dt = \cos x\cdot dx$}$$

This is the logic behind it but to not disturb yourself in the future, multiply both sides by $dx$, $$\cfrac{df}{dx} = g(x)\implies df=g(x)\cdot dx$$

3

Let $y=f(x)$ be a real function. If $f(x)$ is differentiable at $x_0$, then the the expression $$dy=f'(x_0)dx$$ is called the differential of $f$ at $x_0$. Or using the Leibniz's notation for the derivatives

$$dy=\left. \frac{df}{dx}\right\vert _{x_{0}}\; dx$$

For a generic $x$, we thus have

$$dy=f'(x)dx=\frac{df}{dx} dx$$

In the picture below this equation in $dx,dy$ represents the tangent line to the graph of $f(x)$ at $x_0$ in the translated coordinates system $dx,dy$. Both $dy$ and $dx$ are interpreted as infinitesimals. The differential $dy$ is approximately the change of $y$ when $x$ changes by an arbitrary small quantity $dx$.

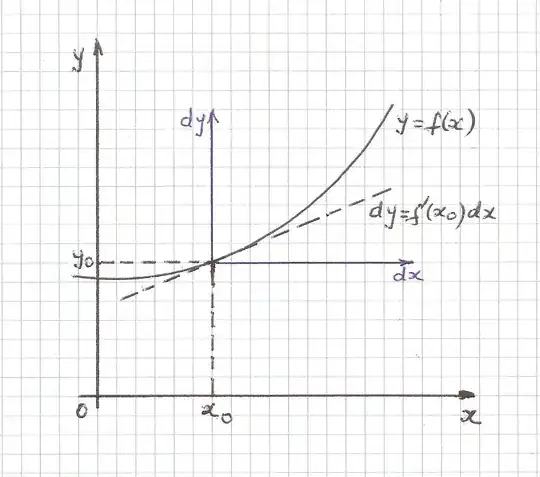
enter image description here

In the present case we have the function $t=f(x)=\sin x$, whose derivative is $$t^{\prime }=f^{\prime }(x)=\frac{df}{dx}=\cos x.$$ So, the diferential $dt$ is

$$dt=f^{\prime }(x)dx=\frac{df}{dx}dx=\cos x\;dx.$$

Further information on the answer to the question What is, how do you use, and why do you use differentials? What are their practical uses?

Community
  • 1
Américo Tavares
  • 38,602
2

If $t=\sin x$ then $t$ is a function of $x$ so $\frac{\mathrm{d}t}{\mathrm{d}x}=\cos x$ and hence $\mathrm{d}t=\cos x\mathrm{d}x$.