2

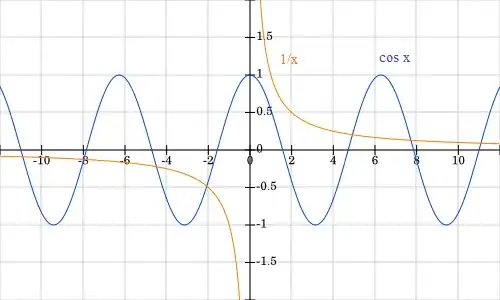
To finding the roots of $x \cos{x}-1=0$ we can write the equation as $$ f(x)=x \cos{x}-1=0 \to x \cos{x}=1 \to \cos{x}=\frac{1}{x} \to \cos{x}-\frac{1}{x}=u(x)-v(x)=g(x)=0 $$ The roots of $f(x)$ are exactly the same roots of $g(x)$. But $f(x)\ne g(x)$. How can it be correct?

enter image description here

Edit: My question is: Can we always simplify the equation (changing $f(x)=0$ to $u(x)-v(x)=0$) to finding the roots?

Edit 2: The main problem is that it is much easier to finding the roots graphically by writing $f(x)$ as difference between two functions $u(x)-v(x)$. Then the roots of $f(x)$ are the intersections of the two functions $u(x)$ and $v(x)$.

Edit 3: The problem is NOT where the two functions $f(x)$ and $g(x)=u(x)-v(x)$ obtained from $f(x)$ by adding or multiplying in the right and left of $f(x)=0$ are defined. The problem is are the roots of $f(x)$ equal to the roots of $g(x)$ or intersections of the two functions $u(x)$ and $v(x)$? Are there counterexamples in which the the roots of $g(x)=u(x)-v(x)$ are not equal to original function $f(x)$?

Edit 4: Can we eliminate $x/x$ from $(x \cos{x})/x=1/x$ to obtain $\cos{x}- (1/x)=0$ ? I think I shouldn't do that. But in my textbook the author does that.

enter image description here

Dante
  • 1,908

4 Answers4

1

Hint: Are both f(x) and g(x) defined for all x?

If not, are f(x) and g(x) the same?

Try to remember what is the necessary condition for dividing both sides of equation by an algebraic expression.

Mythomorphic
  • 6,008
0

they intersect in those points- two functions don't have to be identical to have common zero points see it for yourself http://www.mathsisfun.com/data/function-grapher.php also when you divided by x you excluded the possibility of x=0.

To answer your edit:

I'm not sure what do you mean by simplifying the equation; you set f(x)=0 because you want to find points where f(x)=0, where it intersects the x axis; if for instance your equation is: f(x)=5x+3 then to find the roots you set 5x+3=0(in this case there is only 1 root of course), for sin or cos functions there is an infinite number of them.

If I understood correctly - you want to change f(x) to h(x)-g(x).Of course you can do that if h(x)=f(x)+g(x), but I see no useful applications in finding roots with that.

Oh so you mean THAT, I thought that when you set g(x)=cosx - 1/x , then h(x)= xcosx-1-(cosx-1/x)=cosx(x-1/x)

...anyway that's the whole point - when you set f(x)=0 you eventually get to f(x) = g(x)-/+ h(x) , where g(x) and h(x) are subsets of f(x).

E.g. f(x)=5x+3 - you get the root where 5x=-3, but to do that you need a polynomial(or at least a bynomial) you can't do that with f(x) = 5x or f(x) = cosx...well you can because of 5x+/-0 but it's the same

user155615
  • 29
  • 1
    Your answer definitely has some serious readability issues. Please consider paragraphing. – b00n heT Jun 21 '14 at 13:02
  • I apologise, hope this is better – user155615 Jun 21 '14 at 13:15
  • Thank you, but it is not my answer. One up vote for your effort :) – Dante Jun 21 '14 at 13:18
  • I think it is just the matter of perception- whether you will view the root as a point where the function touches the x axis or a point where two functions that are contained within the original function intersect one another and thank you for your vote – user155615 Jun 21 '14 at 13:26
0

Well in terms of $f(x)$,we can say that $g(x)=\frac{f(x)}{x},x\not= 0$,now clearly if $f(x)$ is $0$ than so is $g(x)$(for $x\not=0$).Though you should always add conditions since you could've said $$x\cos x-1=0\\x\cos x=1\\x=\frac{1}{\cos x}\\x-\frac{1}{\cos x}=u(x)-v(x)=g(x)$$ But clearly for infinitely many values of $x$(zeroes of $\cos x$), $g(x)$ is not defined while $f(x)$ is that is because $g(x)=\frac{f(x)}{\cos x}$

kingW3
  • 13,496
0

In general, if you have $a = b$, you can do the same operation on both sides of the equals sign and the equality stays. In your case, you are looking for $f(x) = 0$. So dividing by $x$ (as long as $x \ne 0$) doesn't change where it is zero, as would be squaring, multiplying by $x^2$, and so on.

If you look at the techniques you use to solve equations, the above operations are your tools. You apply them all the time, probably (by familiarty) not giving a second thought.

vonbrand
  • 27,812