1

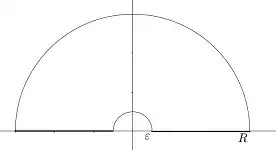
How can I calculate $$\int_0^\infty\frac{\sin x}xdx$$ by integration of a suitable function along the following paths:paths

where $R$ and $\varepsilon$ are the radius of the shown outer and inner semicircle, respectively. This seems to be quite interesting. How would one do that?

user91500
  • 5,606
0xbadf00d
  • 13,422
  • 9
    This is going to be a duplicate post. – Tunk-Fey Jun 13 '14 at 17:41
  • As @Tunk-Fey says, this is bound to have been answered before. But searching for it might not be so easy … Meanwhile, the short answer is to integrate $e^{iz}/z$ around the given path, find that the integral around the big semicircle goes to zero, and the one around the small semicircle has a limit that is easy to find, while the integrals along the straight segments will reduce to $i$ times the integral you are looking for when you write $e^{ix}$ in terms of trigonometric functions and take symmetries into account. Try it yourself, it's good exercise. – Harald Hanche-Olsen Jun 13 '14 at 17:58
  • (Actually, the estimates get a bit easier if you replace the big semicircle by three sides of a square.) – Harald Hanche-Olsen Jun 13 '14 at 18:00
  • @HaraldHanche-Olsen Why I am allowed to make such a replacement? – 0xbadf00d Jun 13 '14 at 19:09
  • Because of the Cauchy integral theorem. The function has no singularities on or within the closed curve formed by the semicircle and the three sides of a square. – Harald Hanche-Olsen Jun 14 '14 at 09:05

1 Answers1

3

Note that $$ \int_0^\infty\frac{\sin x}xdx = \frac 12 \int_{-\infty}^\infty\frac{\sin x}xdx = \frac 12 \Im\left\{\int_{-\infty}^\infty\frac{e^{ix}}xdx\right\} $$ Where $\Im$ denotes the imaginary part. Let $\gamma_R$ be the outer semicircle, let $\gamma_I$ be the part of the contour on the real line (from right to left), and let $\gamma _\epsilon$ be the inner semicircle (clockwise). Since there are no singularities inside the contour, we have $$ \int_{\gamma_R} + \int_{\gamma_I} + \int_{\gamma_\epsilon} = 0 $$ You should be able to argue that $\int_{\gamma_R} \to 0$, so that $$ \lim_{R\to\infty}\lim_{\epsilon \to 0} \left(\int_{\gamma_I} + \int_{\gamma_\epsilon} \right) = 0\implies\\ \int_{-\infty}^\infty \frac{e^{ix}}{x}\,dx = \frac 12 \cdot 2 \pi i \cdot \text{Res}\left(\frac{e^{iz}}{z},z=0 \right) $$ To compute $\text{Res}\left(\frac{e^{iz}}{z},z=0 \right)$, we take the $1/z$ coefficient of the Laurent-expansion of $e^{iz}/z$ centered at zero. The expansion is given by $$ \frac{1}{z}\left(1 + (iz) + (iz)^2/2 + (iz)^3/6 + \cdots\right) = \frac 1z + i - z/2 - iz^2/6 + \cdots $$ So that $\text{Res}\left(\frac{e^{iz}}{z},z=0 \right) = 1$.

So, we conclude that $$ \int_{-\infty}^\infty \frac{e^{ix}}{x}\,dx = \frac 12 \cdot 2 \pi i = \pi i $$ So, taking the imaginary part and halving the result, we conclude that $$ \int_0^\infty\frac{\sin x}xdx = \pi/2 $$

Proof that $\int_{\gamma_R} \to 0:$ In fact, this follows from Jordan's lemma

We may parameterize the integral as $$ \int_{\gamma_R} = \int_0^\pi \frac{e^{i Re^{i\theta}}}{Re^{i\theta}} iR\,d\theta $$ We note that $$ \left|\int_0^\pi \frac{e^{i Re^{i\theta}}}{Re^{i\theta}} iR\,d\theta\right| \leq \int_0^\pi \left|\frac{e^{i Re^{i\theta}}}{Re^{i\theta}} iR\right|\,d\theta = \int_0^\pi \left|e^{i Re^{i\theta}}\right|\,d\theta \\ = \int_0^\pi \left|e^{i R\cos \theta}e^{-R\sin \theta}\right|\,d\theta = \int_0^\pi e^{-R\sin \theta}\,d\theta $$ The fact that this approaches $0$ as $R \to \infty$ is proven in the wikipedia link.

Ben Grossmann
  • 225,327