1

$$\int_{0}^{+\infty}\frac{\sin x}{x}dx$$

My start:

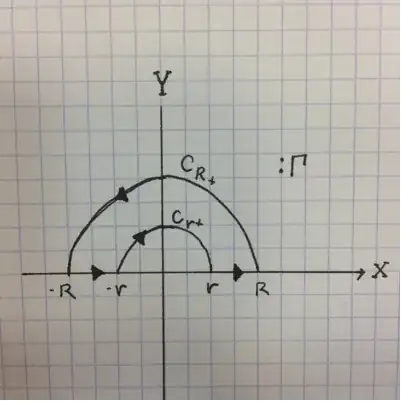
Zero is a singular point, Let's define $g(z):=(e^{iz})\big/z$

$$\int_{\Gamma}\frac{e^{iz}}{z}dz=\\ \int_{-R}^{-r}\frac{e^{ix}}{x}dx+\int_{C_r^+}\frac{e^{iz}}{z}dz+\int_{r}^{R}\frac{e^{ix}}{x}dx+\int_{C_R^+}\frac{e^{iz}}{z}dz$$

$$=\int_{r}^{R}\frac{e^{ix}-e^{-ix}}{x}dx+\int_{C_r^+}\frac{e^{iz}}{z}dz+\int_{C_R^+}\frac{e^{iz}}{z}dz$$

from here I'm stuck the final answer should be $\pi /2$

$$(*)\lim\limits_{r\to 0}\int_{C_r^+}\frac{e^{iz}}{z}dz$$

$$(**)\lim\limits_{R\to 0}\int_{C_r^+}\frac{e^{iz}}{z}dz$$

enter image description here

3SAT
  • 7,512
  • The LHS = 0 - no residues - as you surely know. You need to evaluate - again, as you surely know - the limits of $()$ and $(*)$. So write out the integrals explicitly. The integrals are over semi-circles: parametrize them by $\theta$: $z= re^{i\theta}$ and $z= Re^{i\theta}$. – peter a g Jan 31 '16 at 15:44
  • @peterag $\pi /2$, this is what the book says – 3SAT Jan 31 '16 at 15:47
  • Oh sorry - I misread the question: I thought you wanted the integral over the entire real line. Yes $\pi/2$. (I just edited out the offending line above.) Over the entire real line it is $\pi$. – peter a g Jan 31 '16 at 15:49
  • 1
    May be useful: http://math.stackexchange.com/questions/594641/computing-int-infty-infty-frac-sin-xx-mathrmdx-with-residue-calc – Enrico M. Jan 31 '16 at 16:00
  • 1
    And: http://math.stackexchange.com/questions/833129/calculate-int-0-infty-frac-sin-xxdx-by-integration-of-a-suitable-function?lq=1 – Enrico M. Jan 31 '16 at 16:00
  • @KimPeek Thanks I am voting to close my question as duplicate – 3SAT Jan 31 '16 at 16:05
  • 1
    and see here http://math.stackexchange.com/questions/5248/solving-the-integral-int-0-infty-frac-sinxx-dx-frac-pi2 – Dr. Sonnhard Graubner Jan 31 '16 at 16:07

0 Answers0