Intuitively, why does $\int_{-\infty}^{\infty}\sin(x)dx$ diverge?

Question

According to Wolfram Alpha, $\int_{-\infty}^{\infty}\sin(x)dx$ does not converge.

This makes no sense to me, intuitively, which I'll justify with a plot:

As we see, the positive and negative areas 'cancel out', so, for any $\alpha \in \mathbb{R}$, $\int_{-\alpha}^{\alpha}\sin(x)dx=0$ (I'm just thinking geometrically- in no way is this supposed to be a rigourous justification).

So, why is is that $\int_{-\infty}^{\infty}\sin(x)dx$ diverges?

A natural and intuitive reason, more than a rigourous one, would be best.

Thanks

Answer 1

The integral is $$ \lim_{a \to \infty}\lim_{b \to \infty}\int_{-a}^b \sin x \, d x $$ If you keep one fixed and vary the other limit of integration, there is no limit, the integral fluctuates between $-1$ and $1$. The value doesn't have to blow up for there not be a limit.

Answer 2

It has to do with how improper integrals of this type are defined. Normally, one defines (for continuous functions $f(x)$, for instance) $$\int_0^\infty f(x) \, dx = \lim_{b\to\infty} \int_0^b \! f(x)\, dx,$$ whenever that limit exists. A natural extension is to then define $$\int_{-\infty}^0 f(x) \, dx = \lim_{a\to\infty} \int_a^0 \! f(x)\, dx,$$ (or if you prefer, $\int_{-\infty}^0 \! f(x) \, dx = \int_0^\infty f(-x)\,dx$) whenever that limit exists.

Finally we define $\int_{-\infty}^{\infty}\! f(x)\, dx = \int_{-\infty}^0 \!f(x)\, dx + \int_0^{\infty} \! f(x)\, dx$, because we want all the typical rules of integration to hold for infinite integrals whenever they make sense. As a result, we see that these two limits are taken independently of one another.

What your intuition is currently pointing to is this:

$$\lim_{n\to\infty} \int_{-n}^n \sin(x) \, dx = 0$$ which is true, however if we adopted this definition for double-sided infinite integrals we would no longer be able to split them in the middle, for instance, and so we give up a different intuitive rule which, arguably, is more widely applicable.

Answer 3

"A natural and intuitive reason"... saying that the positive and negative regions cancel out is really just another way of saying $$\infty-\infty=0\ .$$ And this is definitely nonsense - you simply can't do arithmetic with the symbol $\infty$ according to the same rules as you use for ordinary real arithmetic.

Answer 4

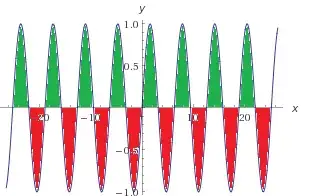
As has already been noted, this is an improper integral and has to be defined in the limit. To look at one half of this integral, we can take the limit of the integral from a fixed point to some other point as that goes to infinity: $$ \lim_{a \to \infty} \int_{x_0}^a {sin(x)}dx$$ for any $x_0$, not necessarily 0.

But this does not converge; we define convergence to be only if the sequence gets arbitrarily close to the point to which it converges. The idea is that, the farther you look, the closer you'll get, no matter what value you choose. So, if you pick some point of the sequence out yonder, and it is yea distance from the limiting point, you shouldn't be able to find some other point out further in the sequence, and have it be farther away from the limiting point, because you were already that close to the limiting point.

But this limit doesn't do that. It gets arbitrarily close to zero, even coinciding, and then gets farther away again. It goes up and down and never "settles in" to any fixed point. So this integral does not converge.

As has again been noted, if we were to look at the integral symmetrically, i.e., define it as $$\lim_{a\to\infty} \int_{-a}^a sin(x) dx$$ then they would cancel out at every point and would be zero no matter where you looked, so this would converge. Again, however, this would violate another rule that we like to demand of improper integrals, namely, that you can split them down the middle, i.e. $$\int_{-\infty}^\infty sin(x)dx = \int_{-\infty}^{x_0} sin(x)dx + \int_{x_0}^\infty sin(x)dx$$ for any point $x_0$, after these integrals have been suitably defined. So, if any one of these integrals is not defined, then neither should the original one be.

So I hope that intuitively explains it for you.

Answer 5

Yes you are right the positive and the negative cancel out. But only if you chose your two boundary lines at multiples of $\pi$, so that for each positive there is a corresponding negative. Consider if you had the boundary fro $0$ to $\frac{\pi}{2}$ then they would not cancel.

So imagine this, we start at $0$ and move in the positive $x$ axis, the area starts to increase until we reach $\frac{\pi}{2}$ then the negative appears and begins to cancel, so the area is now decreasing until it reaches $0$, but then there is another positive region so it increases again, etc so the area just oscillates between $1$ and $0$ over and over again. So it does not converge, its like $1-1+1-1+1-\cdots$ you could also say the positive and negative cancel out here, but if you take it term by term you get $1,0,1,0 \ldots$ and this does not diverge.

You may argue that one should go symmetrically in the positive and negative directions, this is the Cauchy principle value and in this case is $0$, but the definition of an improper integral is the both the positive and negative directions must exist independently.

Answer 6

The areas cancel out because you've chosen to draw it that way. You could have drawn it with a green upper lobe at each end in which case you'd say there's more green than red and they don't cancel. The value of the integral needs to be independent of the little piece you've chosen to draw.

Answer 7

Since we know that $\sin x$ is a odd function. And we also know from the property of definite integral that if a function is odd then limit from (-a) tends to (+a) integral f(x) dx = 0 and we know that sin x is a odd function therefore limit from (-infinite ) tends to (+infinite ) Integral sin x dx = 0