Background: This is another proof that the fresnel integrals $C(\infty)$ and $S(\infty)$ are 1/2 from Hobson, Riley, Bence, Mathematical Methods chapter 25.8 the stationary phase method.
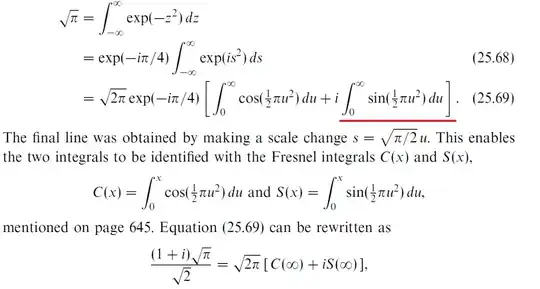 According to here, the integral leading to the underlined does not equal 0 but diverges. According to here the obvious but wrong answer that it equals 0 for being odd is right if you say it's the Cauchy principal value of an ill defined integral. However in the above proof, they evaluated the odd integral to equal twice the integral from zero. Is there any explanation for why and could I do this to any improper infinite integral?
$$\int_{-\infty}^{\infty}\sin(\frac{1}{2}\pi u^2)\text{du}=2\int_0^{\infty}\sin(\frac{1}{2}\pi u^2)\text{du}$$
According to here, the integral leading to the underlined does not equal 0 but diverges. According to here the obvious but wrong answer that it equals 0 for being odd is right if you say it's the Cauchy principal value of an ill defined integral. However in the above proof, they evaluated the odd integral to equal twice the integral from zero. Is there any explanation for why and could I do this to any improper infinite integral?
$$\int_{-\infty}^{\infty}\sin(\frac{1}{2}\pi u^2)\text{du}=2\int_0^{\infty}\sin(\frac{1}{2}\pi u^2)\text{du}$$