In the inversive geometry exercise below (from Geometry Revisited by Coxeter and Greitzer), the solution refers to the point pair $(L, O)$ as the Jacobian of the two point pairs $AC$ and $BD$. I was (and am) vaguely aware of at least two other "Jacobian's": the (I'm quoting Wikipedia here) matrix of all first order partial differentials of a vector valued function and; 2) Jacobian elliptic functions. The exercise follows, but my question is simply if these (and possibly other) uses of the term Jacobian is only because of the common link being the mathematician Carl Gustav Jacobi, or is there some deeper link relating these concepts?
Here is the problem I referred to and my rendition of the book's solution:
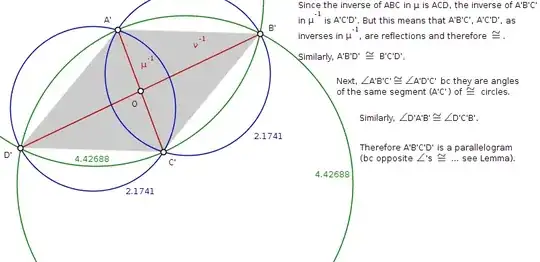
Any four distinct points A, B, C, D can be inverted into the vertices of a parallelogram $A'B'C'D'$ (including, as one possibility, a degenerate parallelogram in which the four vertices lie on one line, but still $A'B' = D'C'$ and $A'D' = B'C'$). Hint: Consider separately the three cases (i) $AC // BD$; (ii) $AB // CD$ or $AD // BC$; (iii) A, B, C, D not concyclic.
The case of interest with respect to Coxeter and Greitzer's use of the term 'Jacobian' is the third. The diagrams below give my rendition of the book's solution for this case: