The area of two intersecting circles.

Question

Two circles with centers $A$ and $B$ of radius $10$ intersect at points $B$ and $C$ such that $AB = 16$. $\angle BAC=\angle ABC = 0.64\,\operatorname{rad}$ and $\angle ACB = 1.86\,\operatorname{rad}$. The arc length $CD = 12.87$.

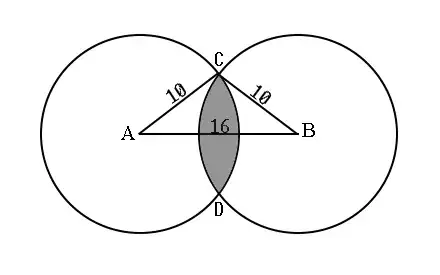
Diagram

I need to find the area of the shaded region and I can't think of any way to do it.

See this Area of intersection between two circles. It can help you. — Jika, May 26 '14 at 17:48
@Jika In that question, the circles are a radius distance apart. — usama8800, May 26 '14 at 17:53
Yes but it is simply a hint. It can give you a way of thinking to solve your problem. @usama8800 — Jika, May 26 '14 at 18:00

score 3 · Accepted Answer · answered May 26 '14 at 18:02

If you draw the line segment from $C$ to $D$, it divides the shaded region into two pieces called circular segments. One of the circular segments is a segment of the circle with center at $A$, and the other is a segment of the circle with center at $B$.

You can see here -- http://mathworld.wolfram.com/CircularSegment.html -- how to compute the area of a circular segment.

score 0 · Answer 2 · answered Dec 03 '23 at 17:13

Though some clever trigonometry, algebra, and substitutions, one can derive a general solution to this problem. This problem was solved by Artemas Martin with a solution published in the Analyst (https://www.jstor.org/stable/2635978).

The key idea is to consider one circle fixed and the other with variable radius. Examining how a differential increase in radius relates to a differential increase in the intersection area you will obtain the following relationship.

$$dA = 2x \cos^{-1}\left(\frac{x^2 + a^2 - r^2}{2ax}\right)dx $$ where x is the variable radius, r is the fixed radius, and a is the distance between their centers. Note the limits of integration are r-a and x.

Through some nonobvious manipulations (perhaps even some kind of wizardry) this integral has the following solution (refer to paper for a rough sketch, but some details you will have to work out on your own).

$$A = x^2\cos^{-1}\left(\frac{x^2 + a^2 - r^2}{2ax}\right) + r^2\cos^{-1}\left(\frac{a^2 + r^2 - x^2}{2ar}\right) - a\sqrt{r^2 - \left ( \frac{a^2 + r^2 - x^2}{2a}\right )^2}$$

Substitute x = R for a specific radius to determine the area of intersection.

Note.

There is a typo in the paper in one step of the derivation. Specifically the last equation on the first page. The right hand side should read $$r^2 \cos^{-1}\left(\frac{y}{2ar}\right) - \frac{1}{2} \sqrt{4a^2r^2 - y^2}$$

The area of two intersecting circles.

2 Answers2