26

This is a soft question. I'm searching for examples of mathmatical statements (preferably in number theory, but other topics are also fine), that seem to be true, but are actually not. Statements where observing some examples would let you think it is always true, but then there is a well hidden counter-example.

If Riemann's $\zeta$ function had a zero beside the critical line, this would be such an example I'm looking for. Or if Fermat's Last Theorem would be false.

Do you know any such surprising counter-exmaples?

Leif Sabellek
  • 1,783
  • 12
  • 17
  • 3
    See the prime generating polynomials: http://mathworld.wolfram.com/Prime-GeneratingPolynomial.html – Amzoti May 26 '14 at 12:56
  • 2
    The number of primes $\le x$ of the form $4k+3$ is never greater than the number of primes $\le x$ of the form $4k+1$. Please see Prime Number Races. Counterexamples are actually not rare, but the first one is big. – André Nicolas May 26 '14 at 13:15
  • 1
    Fermat's Last Theorem is proven true... – Platonix May 26 '14 at 13:21
  • If $p$ is prime, then $2^p-1$ is not divisible by $p^2$. See Wieferich primes. – André Nicolas May 26 '14 at 13:24
  • This rings a bell...duplicate? – daniel May 26 '14 at 13:57
  • 6
    There are some nice examples in this thread. – Viktor Vaughn May 26 '14 at 14:05
  • 5
    All prime numbers are odd :-) – gnasher729 May 26 '14 at 16:32
  • 1
    @gnasher729 And every positive integer divisible only by 1 and itself is prime! – David Richerby May 26 '14 at 17:02
  • $\prod_{i=0}^n(x-i)$ is zero for $x=0, ... n$ but not thereafter. – Jack M May 26 '14 at 23:36
  • The best example that I know is the Gauss conjecture about two curves, that Liouville proved he was wrong. The number that proves Gauss was wrong is estimated to be ridiculously long. Some day I wrote an answer =) – GarouDan May 27 '14 at 22:14
  • One of the important surprises in number theory that I like, Gauss' updated approximation for the number of primes below $x$, $$ \pi(n) \sim \operatorname{Li}(n) = \int_2^n\frac{\mathrm{d}x}{\ln x}. $$

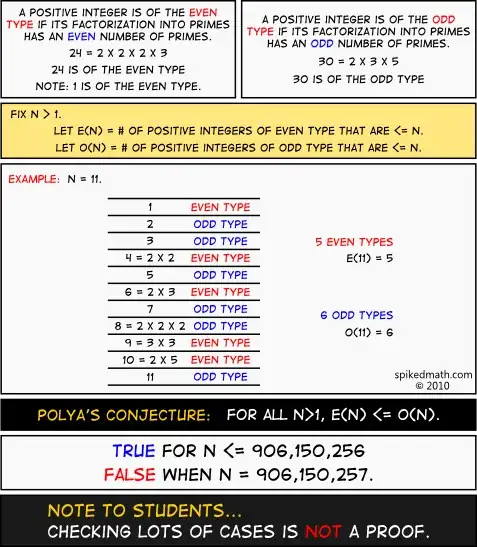
    For all values of $n$ that we can check, $\pi(n) < \operatorname{Li}(n)$. "As a result, many prominent mathematicians, including no less than both Gauss and Riemann, conjectured that the inequality was strict."

     – Bennett Gardiner May 27 '14 at 23:55
  • However, Littlewood (1914) proved that the inequality reverses infinitely often for sufficiently large $n$, and Skewes then showed that the first crossing point must occur before $$n= 10^{10^{10^{34}}}$$ which is now known as Skewes number. This bound has since been lowered to $10^{371}$. – Bennett Gardiner May 27 '14 at 23:55

8 Answers8

50

The following spikedmath is cute.

SM

The books "Counterexamples in Topology" by Steen and Seebach as well as "Counterexamples in Analysis" by Gelbaum and Olmstead have some that are surprising when you first see them.

Hakim
  • 10,213
Batman
  • 19,390
24

For every $n$ $$\int_0^\infty 2 \cos(x) \prod_{i=0}^n\frac{\sin\frac{x}{2i+1}}{\frac{x}{2i+1}}\,dx=\pi/2$$

Is it true? Well, for every $n$ less than 56, but after...

An example of Borwein integral.

sas
  • 3,117
  • 1
  • 17
  • 29
11

Pierre de Fermat conjectured that all Fermat numbers were prime, and a similar mistaken conjecture can be made for most pseudoprimes (Catalan, Fibonacci, Euler, Wieferich, etc.). Also see Euler's sum of Powers conjecture , and the Polya conjecture.

Platonix
  • 701
  • 1
  • 4
  • 21
7

Fermat's ‘little’ theorem states that if $n$ is prime, then $$a^n\equiv a\pmod n\tag{$\ast$}$$ holds for all $a$. The converse, which is false, states that if $(\ast)$ holds for all $a$, then $n$ is prime.

Counterexamples to this converse are uncommon; the smallest is $n=561$.

MJD
  • 65,394
  • 39
  • 298
  • 580
6

The largest odd value of $n$ such that regular $n$-gons are constructable by compass and straight edge is $n=1~431~655~765$.

There is one known exception: $n=4~294~967~295$.

All in all, there are currently only $31$ known constructable regular polygons with an odd number of sides. Prior to Gauss, the largest odd-sided constructable regular polygon was just the pentagon. No doubt much of the numerological and mystical lore surrounding the pentagon and pentagram can be traced back to observations by the ancients that this five sided shape represented some fundamental boundary between the world of finite imperfect man on one side, and the perfect and infinite on the other.

David H
  • 29,921
  • 2
    I'd expect the ancients were smart enough to construct the regular $15$-gon from the triangle and pentagon. – Daniel Fischer May 26 '14 at 17:51
  • 2
    @DanielFischer You're right. Book IV, Proposition 16, of Elements in fact gives the construction. Now editing. – David H May 26 '14 at 17:56
  • 9
    Is there something missing in the first paragraphs, like "for all $n\leq N$"? The first sentence seems to say that the largest odd $n$ for which $P_n$ is true is $n=1,431,655,765$. What is the exception? That $P_m$ is true for $m=4,294,967,295$? If so, then what is the point of the first sentence? – JiK May 27 '14 at 13:43
  • 1
    @JiK Exactly. If the first number was $15$ or something it would make more sense, but the fact that the first number itself is so large makes the point of the first example pointless. All it's saying is that the largest known example of a constructable regular polygon with odd sides is $n = 4294967295$, and the second largest example is $n = 1431655765$.. – MT_ May 28 '14 at 04:22
6

Euler's Sum of Powers Conjecture:

$$a_1^k+\ldots+a_n^k=b^k\qquad\text{with }k>n>1$$

has no solutions in positive integers.

The smallest counterexample is

$$95800^4 + 217519^4 + 414560^4 = 422481^4$$

Toscho
  • 201
4

If $\ n\ $ that $\ ◎(n)=\frac{n+1}{2^x}$ or $\ ◎(n)=\frac{n-1}{2^x}, \ n \in \mathbb{Z^+},\ x \in \mathbb{N}_{\gt 0},\ $then $\ n\ $ is prime.
First counter-example is $\ 92673$.
$◎(n)\ $ is called the cycle length of $n$ , detail see: How to prove these two ways give the same numbers?

Community
  • 1
miket
  • 1,069
  • If change 'then $\ n\ $ is prime' to 'then $\ n\ $ is prime or semiprime' ,then $\ 92673\ $ is the only known counter-example. – miket May 28 '14 at 01:33
4

Lucke numbers of Euler:

For every natural number $n$, the following number is prime: $$n^2-n+41$$

The smallest $n$ for which this conjecture is wrong, is 41 -- naturally.

Toscho
  • 201