A geometric example:
Let $\Omega \in \mathbb{R}^2$ be any bounded connected and open domain. A Neumann Cheeger cut $\gamma$ of this domain is defined to be the curve which separates this domain into two connected disjoints open subdomains $\Omega_1, \Omega_2 \subset \Omega$ (i.e. $\overline{\Omega_1} \cup \overline{\Omega_2} = \overline{\Omega},$ $ \overline{\Omega_1} \cap \Omega = \overline{\Omega_2} \cap \Omega = \gamma,$ $ \Omega_1 \cap \Omega_2 = \emptyset$) such that the follow ratio is minimized:
$R_\Omega^N(\gamma):=\frac{\text{length}(\gamma)}{\min\{\text{surface}(\Omega_1),\text{surface}(\Omega_2)\}}$
Not easy to formulate rigorously but very easy to explain intuitively (even more with a drawing on the black board). Lots of example can be shown quite easily, e.g. if $\Omega$ is a circle then any diameter is optimal, if it is a square then any symmetry axis, etc..
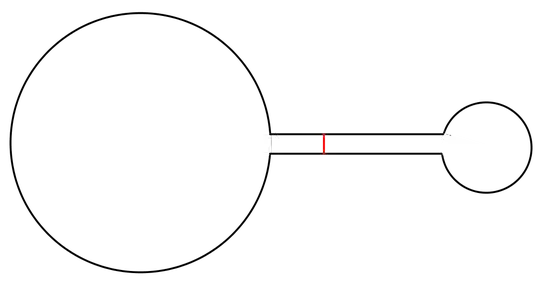
People thoughts a very long time that the optimal curve is attained when $\text{surface}(\Omega_1)=\text{surface}(\Omega_2)$ (I think that also papers were published under this assumption) but this is wrong. A counter example (provided by Klaus Dieter Semmler) can be easily constructed taking two disjoints balls of different radius $r_1,r_2$ and a rectangle joining them, just make the width of the rectangle small enough so that the cut has to be this width.
An image may help :):
Examples: circle ($\infty$ solutions), rectangle isosceles triangle ($2$ solutions), rectangle ($1$ solution))
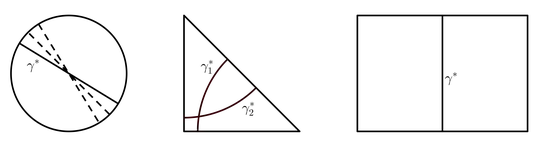 Counter example
Counter example
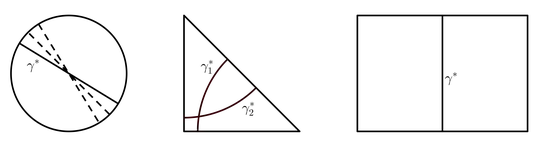 Counter example
Counter example
