Is it $\cfrac{\binom{4}{1} \cdot \binom{48}{4}}{\binom{52}{5}}$?
The way to choose 1 of 4 aces * the way to choose 4 cards from the remaining non-aces, divided by 52 choose 5 (total)?
I know it's the total of the probability of the event over the probability of the total, but I'm not sure about the top part.
Do you want the probability of $exactly$ one ace? Or just the probability of an ace appearing in a 5-card hand?
If you want exactly one ace, then your answer is correct. $\binom{52}{5}$ is the number of 5-card hands in the deck, and you have 4 choices for which ace to include (hence, $\binom{4}{1}$), and 48 choose 4 choices for the other 4 cards (hence, $\binom{48}{4}$).
If, instead, you want the probability of at least one ace appearing in a 5-card hand, we do things differently. The easiest answer is to find the probability of getting $no$ aces in a 5-card hand.
This probability is $$\frac{\binom{48}{5}}{\binom{52}{5}},$$ for we have 48 choose 5 possible hands with no aces.
Then the solution to the problem - that is, the probability of at least one ace appearing in a 5-card hand - is one minus the complement: $$ 1 - \frac{\binom{48}{5}}{\binom{52}{5}}.$$
I should perhaps note that the accepted solution appears incorrect.
The distribution of the number of ace cards in a 5-card hand is a problem in sampling without replacement ... which leads to a Hypergeometric distribution.
Imagine an urn contains a total of $T$ balls, $r$ of which are red $(r<T)$. The experiment proceeds by drawing one-by-one a sample of $n$ balls from the urn without replacement $(n<T)$. Interest lies in determining the pmf of $X$, where $X$ is the number of red balls drawn. Then, the pmf of $X$, $P(X=x)$ is:
$$f(x)=\frac{\left( \begin{array}{c} n \\ x \\ \end{array} \right) \left( \begin{array}{c} T-n \\ r-x \\ \end{array} \right)}{\left( \begin{array}{c} T \\ r \\ \end{array} \right)}$$
In our example, the 'urn' is the deck of $T=52$ playing cards, and the 'red balls' are the ace cards, so $r=4$. There are $n=5$ cards in a hand. Therefore, the pmf of the number of ace cards in a hand of 5 cards is given by:
$$f(x)=\frac{\left( \begin{array}{c} 5 \\ x \\ \end{array} \right) \left( \begin{array}{c} 47\\ 4-x \\ \end{array} \right)}{\left( \begin{array}{c} 52 \\ 4 \\ \end{array} \right)}$$
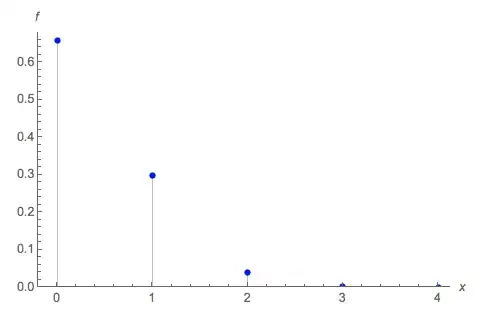
where $X = \{0,1,2,3,4\}$.In the case of just one ace, $P(X=1) = \frac{3243}{10829} \approx 0.299474$.
The following diagram plots the pmf of the number of aces in a hand of 5 cards:
Seems to me that both answers are correct. The first method is just written on a variant of the hypergeometric distribution pmf formular.enter image description here
If I'm not mistaken this form is equel to the one suggested above:enter image description here
