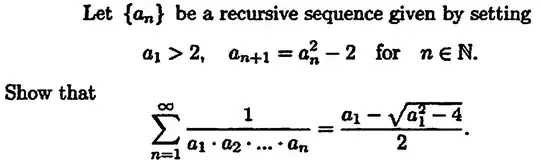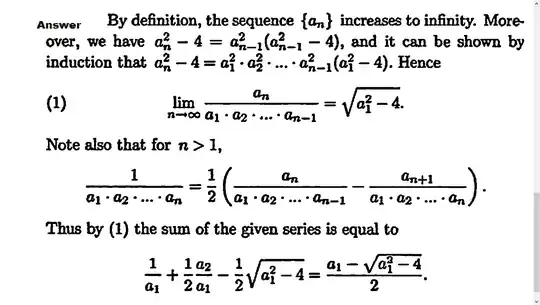For $x_{n+1}=x_n^2-2$, show $\lim_{n\to\infty}\frac{x_n}{x_0x_1\cdots x_{n-1}}=2$

Question

Suppose $x_0:=2\sqrt{2}$ and $x_{n+1}=x_n^2-2$ for $n\ge1$.

We have to show $$\lim_{n\to\infty}\frac{x_n}{x_0x_1\cdots x_{n-1}}=2$$

Establishing convergence is pretty direct but I'm having trouble evaluating the limit. I have tried using the relation $\frac{x_{n}}{x_{0}x_{1}\cdots x_{n-1}}=\frac{x_{n-1}^{2}-2}{x_{0}x_{1}\cdots x_{n-1}}=\frac{x_{n-1}}{x_{0}x_{1}\cdots x_{n-2}}-\frac{2}{x_{0}x_{1}\cdots x_{n-1}}=\cdots=\frac{3}{\sqrt{2}}-2\sum_{k=1}^{n}\frac{1}{x_{0}x_{1}\cdots x_{k}}$ but that doesn't really shed light on the exact value of the limit.

Any and all help appreciated. Thanks!

Answer 1

Note first that $x_n\geq1$ for every $n$. So we may define $t_n$ by the formula $$t_n=\cosh^{-1}\left(\dfrac{x_n}{2}\right)=\ln\left(\frac{x_n+\sqrt{x_n^2-4}}{2}\right)$$ So that $x_n=2\cosh(t_n)$. It follows that $$ 2\cosh(2t_{n+1})=x_{n+1}=4\cosh^2(t_n)-2=2 \cosh(2t_n). $$ Thus $t_{n+1}=2t_n$. It follows that $t_n=2^n t_0$, and consequently $$x_n=2\cosh(2^nt_0)=\frac{\sinh(2^{n+1}t_0)}{\sinh(2^{n}t_0)} \quad\hbox{for every $n\geq0$},$$ It follows that $$x_0x_1\cdots x_{n-1}=\prod_{k=0}^{n-1}\frac{\sinh(2^{k+1}t_0)}{\sinh(2^{k}t_0)} =\frac{\sinh(2^{n}t_0)}{\sinh(t_0)}, $$ and finally $$\frac{x_n}{x_0x_1\cdots x_{n-1}}=\frac{2\sinh(t_0)\cosh(2^{n}t_0)}{\sinh(2^nt_0)}.$$ Thus $$ \lim_{n\to\infty}\frac{x_n}{x_0x_1\cdots x_{n-1}}=2\sinh(t_0)=2. $$ since from $\cosh(t_0)=\sqrt{2}$, we get $\sinh(t_0)=1$.

Answer 2

We have recurrence in two variables, $y_0 = 1, y_1 = x_0,$ then $$ x_{n+1} = x_n^2 - 2, \; \; \; y_{n+1} = x_n y_n. $$

So $$ x_0^2 - (x_0^2 - 4)y_0^2 = 4. $$ Induction, $$ x_{n+1}^2 - (x_0^2 - 4) y_{n+1}^2 = (x_n^2 - 2)^2 - (x_0^2 - 4)(x_n y_n)^2 $$ $$ = x_n^4 - 4 x_n^2 + 4 - (x_0^2 - 4) x_n^2 y_n^2 $$ $$ = x_n^4 - (x_0^2 - 4) x_n^2 y_n^2 - 4 x_n^2 + 4 $$ $$ = x_n^2 (x_n^2 -(x_0^2 - 4) y_n^2 ) - 4 x_n^2 + 4 $$ $$ x_n^2 \cdot 4 - 4 x_n^2 + 4 = 4. $$ So, we always have $$ x_n^2 - (x_0^2 - 4)y_n^2 = 4, $$ and $$ \frac{x_n}{y_n} \rightarrow \sqrt{x_0^2 - 4}, $$ as $$ \frac{x_n}{y_n} = \; \; \; \sqrt {x_0^2 - 4} \; \; \; \; + \; \frac{4}{y_n (x_n + y_n \sqrt {x_0^2 - 4})}. $$

Note that the sequence $x_n$ is precisely the type of sequence used in the Lucas-Lehmer Primality test, except with seed $x_0 = \sqrt 8$ instead of that $s_0 = 4.$ With any seed, the technique in the wikipedia article suffices to give a closed form expression for $x_n.$ So I initially asked about the source of the problem, which has a number theory aspect. I expect that we would be unable to find closed form if we switched to $x_{n+1} = x_n^2 - 3,$ for example.

Answer 3

Hint 1: Note that $$ 2\cosh(2t)=4\cosh^2(t)-2 $$ Therefore, $$ x_n=2\cosh(2^nt_0) $$ satisfies the recursion

---

Hint 2: Since $$ \sinh(2x)=\sinh(x)\ 2\cosh(x) $$ we get inductively that $$ \sinh(t_0)\ 2\cosh(t_0)\ 2\cosh(2t_0)\dots2\cosh(2^{n-1}t_0)=\sinh(2^nt_0) $$

---

Finish off with $$ \lim_{n\to\infty}\coth(2^nt_0)=1 $$ for $t_0\gt0$, and $$ 2\sinh\left(\cosh^{-1}\left(\frac{x_0}{2}\right)\right)=\sqrt{x_0^2-4} $$

Answer 4

A related question.

And its answer