11

The coordinate transformation (due to Beukers, Calabi and Kolk)

$$x=\frac{\sin u}{\cos v}$$

$$y=\frac{\sin v}{\cos u}$$

transforms the square domain $0\lt x\lt 1$ and $0\lt y\lt 1$ into the triangle domain $u,v>0,u+v<\pi /2$ (in Proofs from the BOOK by M. Aigner and G. Ziegler).

Since the invert transformation is

$$u=\arccos \sqrt{\dfrac{1-x^{2}}{1-x^{2}y^{2}}}$$

$$v=\arccos \sqrt{\dfrac{1-y^{2}}{1-x^{2}y^{2}}}$$

it is easy to see that three of the vertices (although not belonging to the domain) are transformed as follows:

$$(x,y)=(0,0)\mapsto (0,0)=(u,v),$$

$$(x,y)=(1,0)\mapsto (\pi /2,0)=(u,v),$$

$$(x,y)=(0,1)\mapsto (0,\pi /2)=(u,v).$$

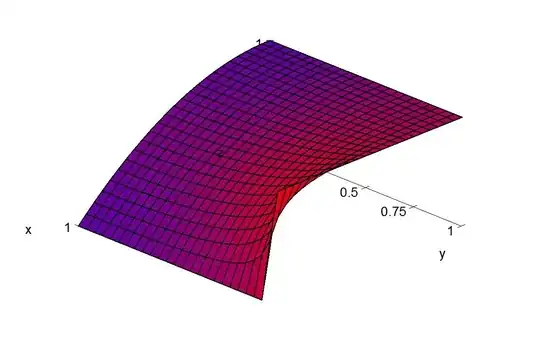
Question 1 - But how is the fourth vertex $(x,y)=(1,1)$ transformed? In the plot below of $\dfrac{1-x^{2}}{1-x^{2}y^{2}}$ seems that the following limit does not exist

$$\underset{(x,y)\rightarrow (1,1)}{\lim }\sqrt{\dfrac{1-x^{2}}{1-x^{2}y^{2}}}.$$

alt text

Question 2 - As a second question I would like to know how can one "discover" a transformation of a square into a triangle such as this. Is there any systematic study of this kind of transformations?

Américo Tavares
  • 38,602
  • @Hans Lundmark: You are right. I've corrected to vertices, that was what I meant. It was an error. @Rasmus: it should read "how is the forth vertex (x,y)=(1,1) transformed". – Américo Tavares Oct 25 '10 at 17:15
  • @Rasmus: That's right. This transformation is presented in the context of evaluating a non trivial double integral over the interior of the square defined above. The transformed integral is a simple double integral over the interior of the triangle I mention. – Américo Tavares Oct 26 '10 at 19:46

1 Answers1

6

Question 1: Setting $u=\pi/2-v$ in your first set of formulas gives $(x,y)=(1,1)$, so that point corresponds to the whole hypotenuse $u+v=\pi/2$.

Question 2: I have no idea. (Luck? Inspiration? Trial and error?)

Hans Lundmark
  • 53,395