Find normal vector of circle in 3D space given circle size and a single perspective

Question

I don't really know what to search up to answer my question. I tried such things as "ellipse matching" and "3d circle orientation" (and others) but I can't really find much. But anyways...

I have this camera tracking a circle in 3d space. All it can see is a skewed and distorted version of that circle. The computer knows the exact size of that circle (like it's radius). The computer can calculate the smallest rectangle (with edges completely horizontal) and find the four points on the rectangle (one point per side) at which the distorted circle touches that rectangle.

How would I go about finding the orientation of the circle? (the direction of the normal vector of the circle).

Some thoughts I have had that the center of the circle must be at the intersection of the diagonals of the rectangle. Is that true to say? And where would I go after this. If someone can help me find a website that explains this instead, that would also be helpful.

EDIT: You also know the angle at which the center of this rectangle is from the camera.

An image would look something like this:

Answer 1

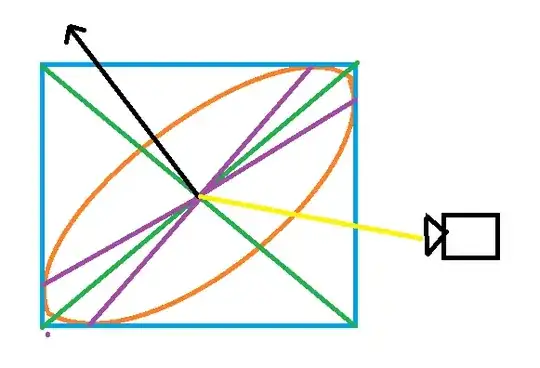
First of all, set up the viewing reference frame, and attach it to the camera. The camera viewing direction and orientation is assumed given, as well as the "focal distance" which is the distance between the center of the camera and the projection plane, which lies between the viewed object and the center of the camera. We can take the center of the camera to be at the origin of the world coordinate frame, and have a reference frame represented by the rotation matrix $V$, so that

$\mathbf{p} = V \mathbf{q} $

where $\mathbf{p}$ is the coordinate vector of a point in $3D$ and $\mathbf{q}$ is the coordinate vector in the camera frame of refence (local frame).

The idea of this solution is as follows: From the image that lies in the projection plane of the camera, connect the origin of the camera to the ellipse that lies in the image plane, and extend these line segments into rays. The collection of the rays forms a cone. Set up a "unknown" plane of the viewed circle. This plane is such that it intersects the cone in a circle, and this circle has a radius of $r$ (which is known).

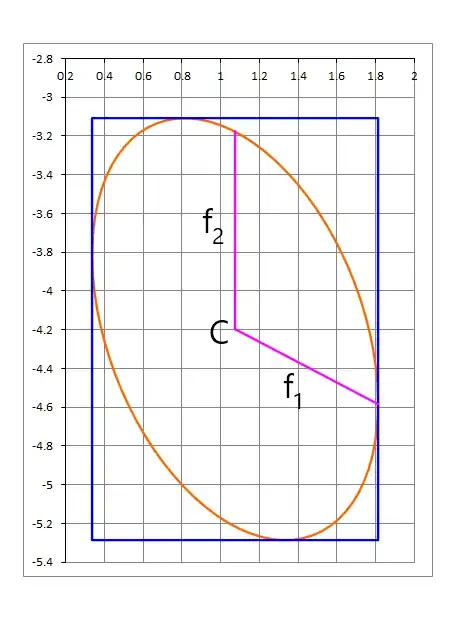
Now, from the given image, we know the $x$ limits, $X_{min}, X_{max}$ and the $y$ limits $Y_{min}, Y_{max}$, and we also know the right touching point $(x_1, y_1)$

From these, the center of the ellipse is

$ \mathbf{C} = (C_x, C_y) = \frac{1}{2} ( X_{min} + X_{max}, Y_{min} + Y_{max} ) $

Using conjugate axes, we define the first conjugate semi-axis as follows

$ \mathbf{f_1} = ( x_1 - C_x , y_1 - C_y ) $

This is a vector pointing from $\mathbf{C}$ to $(x_1, y_1)$. Since the tangent at this point is parallel to the $y$ axis, then the other conjugate semi-axis is

$ \mathbf{f_2} = (0, K) $

So that now, the ellipse is given by

$ \mathbf{E}(t) = \mathbf{C} + \mathbf{f_1} \cos(t) + \mathbf{f_2} \sin(t) $

We can find $K$ from the fact that the maximum $y$ of the ellipse is $Y_{max}$, which implies that

$ Y_{max} = C_y + \sqrt{ (y_1 - C_y)^2 + K^2 } $

And this equation can be easily solved for $K$. ($K$ can be taken as positive or negative).

The ellipse $\mathbf{E}(t)$ coordinates are coordinates in the viewing (projection) plane, whose normal vector is the $Z$ axis of the local coordinate matrix $V$, therefore, in local coordinates, the ellipse is given by

$ \mathbf{q} = \begin{bmatrix} \mathbf{E}(t) \\ \alpha \end{bmatrix} $

$\alpha$ is a constant of the camera that determines the location of the viewing (projection) plane with respect to the center of the camera.

Partitioning $V$ into

$ V = [V_1 , V_2 ] $

where $V_1$ is $3 \times 2$ and $V_2 $ is $3 \times 1 $, we obtain the parametric equation of the ellipse in world coordinates

$ \mathbf{p} = V \mathbf{q} = V_1 \mathbf{E} + \alpha V_2 = V_1 \left(\mathbf{C} + \mathbf{f_1} \cos(t) + \mathbf{f_2} \sin(t) \right) + \alpha V_2 = \mathbf{g_0} + \mathbf{g_1} \cos(t) + \mathbf{g_2} \sin(t)$

The last expression on the right of the above equation can be written in compact form as

$ \mathbf{g_0} + \mathbf{g_1} \cos(t) + \mathbf{g_2} \sin(t) = G \mathbf{w} $

where $ G =\begin{bmatrix} \mathbf{g_1} && \mathbf{g_2} && \mathbf{g_0} \end{bmatrix} $ and $ \mathbf{w} = \begin{bmatrix} \cos(t) \\ \sin(t) \\ 1 \end{bmatrix} $

Hence,

$ \mathbf{p} = G \mathbf{w} $

Note that since $\cos^2(t) + \sin^2(t) - 1 = 0 $ then

$ \mathbf{w}^T Q_0 \mathbf{w} = 0 $, where $Q_0 = \begin{bmatrix} 1 && 0 && 0 \\0 && 1 && 0 \\ 0 && 0 && -1 \end{bmatrix} $

And from this, it follows that the equation of the cone on which $\mathbf{p}$ lies is

$ \mathbf{p}^T G^{-T} Q_0 G^{-1} \mathbf{p} = 0 $

Let $Q = G^{-T} Q_0 G^{-1} $

Diagonalize $Q$ into $Q = R D R^T $, and scale and rearrange diagonal elements of diagonal matrix $D$ (and corresponding vectors in $R$) such that $D$ is of the form

$ D = \begin{bmatrix} D_{11} && 0 && 0 \\ 0 && D_{22} && 0 \\ 0 && 0 && -1 \end{bmatrix} $

with $D_{11} \ge D_{22} \gt 0 $.

The rotation matrix $R$ represents the rotation of the axes of the elliptical cone with respect to the world coordinates. Let $u$ be the position vector of points on the cone surface with respect to this local frame specified by $R$ then

$ \mathbf{p} = R \mathbf{u} $

So that $ \mathbf{u}^T D \mathbf{u} = 0 $

In this frame (the one specified by $R$), we define a plane with normal

$\mathbf{n_0} = [\sin(\theta) \cos(\phi), \sin(\theta) \sin(\phi), \cos(\theta) ]^T $

And such that the plane passes through $\mathbf{u_0} = [0, 0, \beta]^T $

You can convince yourself that the normal vector that will result in a circular section of the cone must have a normal vector that lies in the $x'z'$ plane, i.e. $ \phi = 0 $, and hence

$ \mathbf{n_0} =[\sin(\theta) , 0, \cos(\theta) ]^T $

Two orthogonal unit vectors that span the plane of the circle are

$ \mathbf{u_1} = [\cos(\theta), 0, -\sin(\theta) ]^T $

$ \mathbf{u_2} = [ 0, 1, 0 ]^T $

So that now the equation of the plane is

$ \mathbf{u} = \mathbf{u_0} + [\mathbf{u_1} , \mathbf{u_2}] \mathbf{s} = \mathbf{u_0} + U \mathbf{s} $

where $\mathbf{s} = [s_1, s_2]^T $ is the coordinate vector of a point with respect to the two spanning vectors $\mathbf{u_1}$ and $\mathbf{u_2} $.

Using the above into the equation of the cone in local coordinates, we get

$ \mathbf{u}^T D \mathbf{u} = 0 $

And this leads to

$ (\mathbf{u_0} + U \mathbf{s})^T D (\mathbf{u_0} + U \mathbf{s} ) = 0 $

which expands into

$ \mathbf{u_0}^T D \mathbf{u_0} + 2 \mathbf{s}^T U^T D \mathbf{u_0} + \mathbf{s}^T U^T D U \mathbf{s} = 0 $

The matrix $U^T D U$ is given by

$ U^T D U = \begin{bmatrix} D_{11} \cos(\theta)^2 - \sin(\theta)^2 && 0 \\ 0 && D_{22} \end{bmatrix} $

So, in order to have a circle, we must have these two diagonal elements equal to each other, and hence

$ D_{11} \cos^2(\theta) - \sin(\theta)^2 = D_{22} $

From which we can find $ \theta $ as

$ \theta = \pm \cos^{-1} \left( \sqrt{ \dfrac{ D_{22} + 1 }{D_{11} + 1 } } \right) $

The matrix $U^T D \mathbf{u_0} $ is given by

$ U^T D \mathbf{u_0} = \begin{bmatrix} \beta \sin(\theta) \\ 0 \end{bmatrix} $

and the scalar $\mathbf{u_0}^T D \mathbf{u_0} $ is equal to $ - \beta^2 $.

So that the equation of the circle of intersection becomes

$ D_{22} ( s_1^2 + s_2^2 ) + 2 s_1 \beta \sin(\theta) - \beta^2 = 0 $

Dividing through by $D_{22}$

$ s_1^2 + s_2^2 + 2 s_1 \left(\dfrac{\beta \sin(\theta)}{D_{22}}\right) = \dfrac{\beta^2}{D_{22}} $

Completing the square in $s_1$, the above becomes

$ \bigg( s_1 - \left(- \dfrac{\beta \sin(\theta)}{D_{22}} \right) \bigg)^2 + s_2^2 = \beta^2 \bigg( \dfrac{1}{D_{22}} + \dfrac{\sin(\theta)^2}{D_{22}^2}\bigg)$

Which is a circle centered at $\mathbf{s} = \bigg( - \dfrac{\beta \sin(\theta)}{D_{22}} , 0 \bigg)$ and having the square of radius equal to

$ r^2 = \beta^2 \bigg( \dfrac{1}{D_{22}} + \dfrac{\sin(\theta)^2}{D_{22}^2} \bigg) $

From which, we can determine the unknown $\beta$

$ \beta = \dfrac{r}{ \sqrt{\dfrac{1}{D_{22}} + \dfrac{\sin(\theta)^2}{D_{22}^2}}} $

Now the requested plane normal of the plane of the circle is

$ \mathbf{n} = R \mathbf{n_0} $

where as above

$ \mathbf{n_0} = [ \sin(\theta), 0, \cos(\theta) ] $

And the center of the circle is

$ \mathbf{C} = R \bigg( \mathbf{u_0} + \bigg( - \dfrac{\beta \sin(\theta)}{D_{22}} \bigg) \mathbf{u_1} \bigg) $

So, in summary, there are two possible unit normal vectors to the plane of the circle, each with a corresponding circle center. These two unit normal vectors are generated by taking $\theta$ to be positive in the first case, and negative in the second case.

Answer 2

let's start by assuming your camera has no perspective distortion (which of course isn't true) - so in other words, assuming we have an orthogonal perspective:

So you know the radius of the circle, and you know the four points where the circle touches the rectangle, plus you can get the center by connecting the diagonals of the rectangle (this is true if you have no perspective distortion since the center of the ellipse is equally placed between top and bottom, and side-to-side). So this is what you have.

What we need are two points on the edge of the circle, the center point, and the radius. And then this is what you do (let's say the camera view is of the $yz$ plane):

1. You have point 1: $p_1=(x_1,a_1,b_1)$ where $x_1$ is unknown and $a_1,b_1$ is known (calculated by computer from where it touches the rectangle)...and similarly you have point 2: $p_2=(x_2,a_2,b_2)$.
2. Then you have the center point: $p_c=(0,a_c,b_c)$ (since we have no depth information we arbitrarily place the $yz$ plane at the center of the circle)
3. Now we must have $\|p_1-p_c\|^2=r^2=x_1^2+(a_1-a_c)^2+(b_1-b_c)^2$ from which you can calculate the absolute value of $x_1$ and similarly $\|p_2-p_c\|^2=r^2=x_2^2+(a_2-a_c)^2+(b_2-b_c)^2$ from which you can calculate the absolute value of $x_2$.
4. So now the trick comes in that you have to determine if $x_1$ and $x_2$ should be positive or negative. If you choose $p_1,p_2$ so that they are opposite (in the sense that they have inverse coordinates about the center: $a_1-a_c=a_c-a_2$, $b_1-b_c=b_c-b_2$) then $x_1$ and $x_2$ should have the same absolute value, but opposite signs...so only two possibilities, so maybe some trial and error here, but let's assume you can correctly determine whether $x_1,x_2$ is closer to the camera than the center or further away.
5. Then you have two vectors $v_1=(x_1,a_1-a_c,b_1-b_c)$ and $v_2=(x_2,a_2-a_c,b_2-b_c)$ and taking the cross product of these vectors you will have a vector which is normal to the circle.

So then the next step is to correct for camera perspective - maybe something like this can be a start?: https://stackoverflow.com/questions/1194352/proportions-of-a-perspective-deformed-rectangle