3

Question 1: The volume of a parallelepiped in $\mathbb{R}^n$ with n sides given by the vectors $(x_{1_1}, x_{1_2} ... x_{1_n}), (x_{2_1}, x_{2_2} ... x_{2_n}) ... (x_{n_1}, x_{n_2} ... x_{n_n})$ and diagonal $(x_{1_1} + x_{2_1}+ \cdots + x_{n_1}, x_{1_2} + x_{2_2} + \cdots + x_{n_2}, ..., x_{1_n} + x_{2_n} + \cdots + x_{n_n})$ Is the determinant of the matrix $A = (x_{j, i})$ where i and J are the double sub-scripts on each $x_{i_j}$.

The case where n= 2 has a nice geometric proof. Shown in this diagram:

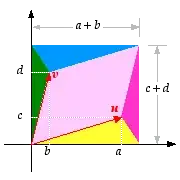
alt text

$u= (a,c)^T$ and $v= (b, d)^T$ then the area of the parallelogram is

$ det \left| [ u | v ] \right| = | ad - bc| $

Is there a "nice" geometric proof for n=3?

The idea behind the n=2 proof is you take the area of the rectangle and subtract the triangles. So, I'm thinking: take the volume of the rectangular solid and subtract tetrahedrons. How many will I need to subtract? Is it possible to draw this?

Question 2: Suppose that (a,b) and (b, a) are points on the unit circle. Find parallelogram with vertices (0,0), (a,b) (a+b, a+b), (b,a) is where $\theta$ is between the x-axis and (a,b).

I know the answer is $|2cos^2 \theta -1|$. I want to get a sense of how difficult this question is. Could an undergrad taking linear for the first time do this? Is it easier if one is asked to prove that the area is $|2cos^2 \theta -1|$ rather than finding it from scratch?

The graphic is from: http://algebra.math.ust.hk/determinant/01_geometry/lecture1.shtml

VividD
  • 15,966
futurebird
  • 6,248
  • 1
    I think a better notation for your double subscripts could be just $x^i_j$. Don't you think so? For me at least, it looks rather bizarre a subscript like $x_{1_2}$. – Agustí Roig Oct 24 '10 at 20:00
  • Yeah, personally subscripts on subscripts (or for that matter superscripts on superscripts) make me commiserate with the people who think math looks complicated. – J. M. ain't a mathematician Oct 25 '10 at 00:18
  • I was concerned a superscript might look like a power in a context where we are doing so much geometry... but perhaps you are right. – futurebird Oct 25 '10 at 11:56

3 Answers3

2

It is a fact of linear algebra that any nonsingular matrix $A$ is a product of "elementary matrices". An elementary matrix $E$ is either (a) an identity matrix with one diagonal entry replaced by an arbitrary $a\ne 0$ or (b) an identity matrix with one off-diagonal zero replaced by some $b\ne 0$. In case (a) the corresponding linear map multiplies volumes by $|a|$, which coincides with $|\det(E)|$, and in case (b) volumes are unchanged by $E$, which can be verified by looking at a two-dimensional figure. It follows that in case (b) the volume factor is $1=|\det(E)|$ as well. By the multiplicativity of determinants it follows that any nonsingular $A:\mathbb R^n\to\mathbb R^n$ multiplies volumes by the factor $|\det(A)|$. The parallelepiped $P$ considered in the question is the linear image of the unit cube; therefore vol$(P)=|\det(A)|$ where the matrix $A$ has the spanning vectors of $P$ in its columns.

Christian Blatter
  • 226,825
1

For question 2, I think it is easy to find the area if you know a bit of trig, not using the linear algebra. But maybe the students are too limited by the class at hand to use another approach.

Ross Millikan
  • 374,822
  • Do you mean in the same manner as the proof? Fining the total area of the rectangle and subtracting triangles? – futurebird Oct 24 '10 at 16:51
  • No, I mean just looking at the triangle in the circle and finding its are from the central angle. It seems it is a problem they did before that way. – Ross Millikan Oct 24 '10 at 16:54
1

Question 2: Since $a=\cos\theta$ and $b=\sin\theta$, it follows from the determinant formula for the area: $$ A = \left| \det\begin{pmatrix} a & b \\ b & a \end{pmatrix} \right| = | \cos^2\theta - \sin^2 \theta |.$$ So I would say this is an easy problem for a linear algebra student.

Hans Lundmark
  • 53,395