1

There are many proofs that the determinant of a 2x2 matrix is $ad - bc$ which is the area of a parallelogram bounded by the row (or column) vectors of the matrix. They come in many forms: plain calculation, induction, proof by picture or geometry, non-computational properties of a determinant and the area. Some of these translate to higher dimensions (a simple search on google/math.SE shows many variations of these).

The determinant for $n$ matrices is often given as a direct computation over permutations:

$$\det A = \sum_{\pi \in S_n} sgn(\pi) \cdot a_{1\pi(1)} \cdot \ldots \cdot a_{n\pi(n)}$$ where $S_n = \{ \pi : \{1,\ldots, n\} \to \{1,\ldots, n\} ~ | ~ \pi \text{ bijective }\} $ and $sgn(\pi)$ the is the parity of the permutation $\pi$, i.e. either $1$ or $-1$.

I wonder if there is an illuminating proof for $n$ dimensions that uses permutations combinatorially, an extension of the proof by skewing areas and volumes and adding or subtracting areas/volumes to correct. I am looking for a proof that is analogous to the binomial theorem, the coefficients of $(x+y)^n$ (each monomial comes from selecting without replacement $m$ 'x' vars in a monomial) and this can be viewed as combining the sub hyper-volumes of a hypercube of edge $x+y$.

Is there an inclusion-exclusion proof over permutations for the sub-hyper-volumes of the hyper-parallelepiped? It may well be an inductive proof where the inductive case involves $n$ overlapping sub-hyper-volumes.

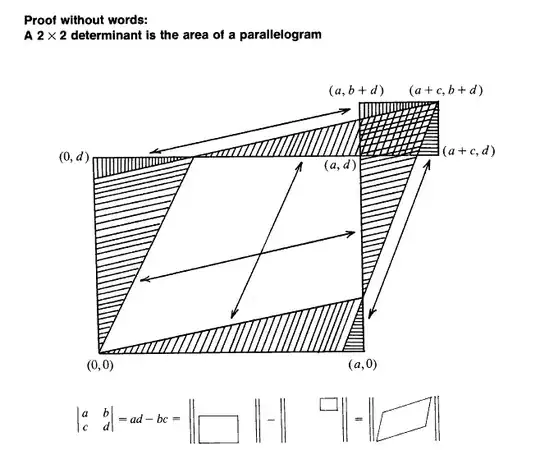
Or more informally, here is a proof by picture using inclusion exclusion of areas for a 2x2 matrix:

area between two vectors is the determinant of the matrix

Is there an analogous picture for the corresponding $n=3$ and the more general mapping to permutations $n$ arbitrary situation? I don't immediately see that adding a vector to the 2 by 2 case translates to doing three versions of 2 by 2 and adding or subtracting accordingly. How do the volumes overlap when they are sheared in three dimensions? (note that the picture proof assumes a particular ordering of magnitude of $a, d > b, c$; presumably the proof works with minor mods for other orderings and considering largest first).

In other words, how can the volumes correspond to terms in the determinant:

$$ \begin{vmatrix} a&d&g\\ b&e&h\\ c&f&i \end{vmatrix} = a\begin{vmatrix}e&h\\f&i\end{vmatrix} - d\begin{vmatrix}b&h\\c&i\end{vmatrix} + g\begin{vmatrix}b&e\\c&f\end{vmatrix} $$

$$= aei - afh - dbi + dch + gbf - gce$$

Mitch
  • 8,591
  • What exactly are you trying to prove? That the $n$-dimensional hyper-parallelipiped spanned by $n$ vectors $v_1, v_2, \ldots, v_n$ can be split into $n!$ simplices, each of which is congruent to one with vertices $0, v_1, v_2, \ldots, v_n$ ? – darij grinberg Oct 22 '18 at 14:36
  • @darijgrinberg I want to prove the usual 'determinant=hypervolume' statement but each term in the sum (from one of $n!$ permutations) would correspond to some subvolume (whatever it might correspond to). They don't have to be congruent. I'd expect that they're not, but maybe you have a proof where they are. In the elementary proof by picture. the subareas are not congruent. – Mitch Oct 22 '18 at 15:32
  • Ah, I see what you mean! – darij grinberg Oct 22 '18 at 15:42
  • OK, slow attempt in progress... $n$ vectors have $n^n$ rectilinear 'boxes' ($2^2 = 4$, $3^3 = 27$ etc). How to get only $2! = 2$, $3! = 6$ 'boxes' to contribute to volume? wedge product is 0 for another coeff from same vector, so only permutations left..but how does this correspond to inclusion exclusion of those boxes? – Mitch Oct 23 '18 at 19:49

0 Answers0