3

I have already tried with $S_3$, and indeed, the product is $(13)$, and $(13)^2=e$

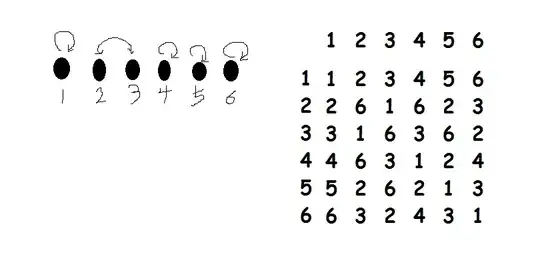
enter image description here

But what about this: I define + in this way:$45=2$,$26=3$, $1$ is the identity. therefore, $123456=2326=233=3$, and as you can see from the picture, the inverse of $3$ is not itself, thus contradicts the statement. My question:
What is wrong with my argument?
And How do you prove the statement?
it seems that my set of numbers perfectly forms a group under the operation I defined via the table above. first it's closed, second there is an identity, third every elements have an inverse. By the way it's commutitive. I tried (45)2=22=6=42=4(52), (45)6=26=3=43=4(56), so associativity seems to be satisfied.

pxc3110
  • 1,410

3 Answers3

5

Note that $x^2=(a_1a_2a_3\cdots a_n)(a_1a_2a_3\cdots a_n)=(a_1a_2a_3\cdots a_n)(a_1^{-1}a_2^{-1}a_3^{-1}\cdots a_n^{-1})$ because inversion is a bijection and the group is abelian.

lhf
  • 216,483
  • If G is of odd order, what can you say about "x" or the product then please? – pxc3110 Apr 25 '14 at 03:01
  • @pxc3110, a group of odd order cannot have an element of order 2, because of Lagrange's theorem. Since $x^2=e$, the only way is $x=e$. But that was not part of your question. – lhf Apr 25 '14 at 03:02
  • @pxc3110, see http://math.stackexchange.com/questions/9311/product-of-all-elements-in-an-odd-finite-abelian-group-is-1. – lhf Apr 25 '14 at 03:06
4

$$a_1a_2a_3\ldots a_n a_1a_2a_3\ldots a_n$$ Let's start by canceling $a_1$. Some other, unique $a_i$ is equal to $a_1^{-1}$. Since the group is abelian, we can move that $a_i=a_1^{-1}$ from the second half over beside the $a_1$ in the first half (everything commutes, so order doesn't matter). So, those cancel, leaving $$a_2\ldots a_na_1\ldots a_{i-1}a_{i+1}\ldots a_n$$ Now we can do the same thing to cancel the $a_1$ on the right, we can just move it over next to the $a_i=a_1^{-1}$ on the left, and they cancel, so now we have $$a_2\ldots a_{i-1}a_{i+1}\ldots a_na_2\ldots a_{i-1}a_{i+1}\ldots a_n$$ Now both $a_1$ and $a_i$ are dealt with, and we're one step closer to the identity. We can do the same with $a_2,a_3,$ and so on.

What I'm writing isn't a rigorous proof, but do you get my drift as to why this works intuitively? Could you turn it into a rigorous proof?

Think about pairing each element with its inverse. Can you show that $x^2=a_1a_1^{-1}a_2a_2^{-1}\ldots a_na_n^{-1}a_1a_1^{-1}a_2a_2^{-1}\ldots a_na_n^{-1}$?

Extended question to consider: why is it that we can't just write $x=a_1a_2\ldots a_n=e$ using the above logic? What is the one thing that could mess that up and make us need another copy of $x$?

Alexander Gruber
  • 26,963
  • thank you sir. And what's wrong with the operation I defined? will the set form a group under this operation? – pxc3110 Apr 25 '14 at 03:18
  • @pxc3110 Like Zarrax said, you haven't defined a group. Are you sure you understand the definition of a group? – Alexander Gruber Apr 25 '14 at 03:21
  • About your extended question: I realized in the first place that some non trivial elements could have itself as its inverse, there fore their product needs not be the identity, is that correct? – pxc3110 Apr 25 '14 at 03:21
  • @pxc3110 Yes, so if you know Cauchy's, you can then say that $x=a_1a_2\ldots a_n=e$ in an abelian group if and only if the order of the group has what property? – Alexander Gruber Apr 25 '14 at 03:35
  • If the finite group is of odd order, the by lagrange's theorem, none of the elements has order of 2, therefore, none of them has itself as its inverse, or all of them can paired together, don't know a thing about Chauchy's though – pxc3110 Apr 25 '14 at 03:42
  • @pxc3110 The point was that if the group has even order, it has an element of order $2$, and on second thought we don't need actually Cauchy's because the group is abelian. So that's the only if. – Alexander Gruber Apr 25 '14 at 03:46
  • I see, by cauchy's, what you said is that if it's even order, then the product is not the identity. So it's the identity only if it's odd. so that's where the only if comes from. Maybe I get it wrong, but if the group is of even, then there may exist three elements of order two, e.g. ABC, if AB=c, then ABC will be the identity. So I think that when it's off odd, then the product x must be identity, if it's even, it may or may not be the identity. By the way, does the identity have an order? – pxc3110 Apr 25 '14 at 06:21
2

What you have defined is not a group.

Hint for your problem: Pair each $a_i$ that you can with its inverse, and multiply to get $1$. Which $a_i$ are left in your product?

Zarrax
  • 44,950
  • Thank you sir. Why is it not group please? I already tried what you said before, but what I concluded was that the product is some element in the group, and its inverse needs not be itself. – pxc3110 Apr 25 '14 at 02:57
  • you have to define all possible products... and you have to make sure they satisfy associativity, commutativity (for an abelian group) and so on. So the products you have given can't be extended to all possible products in such a way that you get an abelian group. – Zarrax Apr 25 '14 at 02:59