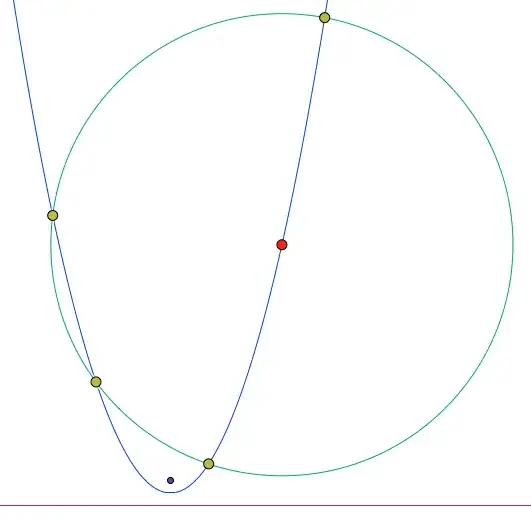
There can be up to four points of intersection
You can apply the generic machinery to intersect conics. That's quite a lot of work, but I doubt there is a shortcut here. Even if you assume $x_0=y_0=c=0$, you are still left with a fourth degree polynomial in $x$. Which makes sense, since you can have up to four points of intersection:
To use that approach, you could formulate your conics as matrices:
$$
C=\begin{pmatrix}
1 & 0 & -x_0 \\
0 & 1 & -y_0 \\
-x_0 & -y_0 & x_0^2+y_0^2-r^2
\end{pmatrix}
\qquad
P=\begin{pmatrix}
2a & 0 & b \\
0 & 0 & -1 \\
b & -1 & 2c
\end{pmatrix}
$$
Explicit formulas
You could also feed that special case into Wolfram alpha to obtain explicit formulas for the four points of intersection, but these formulas are rather complicated, and intermediate values will probably still have to be computed using complex numbers.
How many points of intersection are there?
In a comment below, you asked about when there would be exactly two points of intersection. Consider the picture above. You could make the radius smaller until it no longer intersects the left branch, or you could make it larger until it completely encompasses the lower part of the parabola. In between these situations is the range where you get four points of intersection. And the switchover will occur in a situation where some of these points of intersection come to coincide.
Such multiple solutions can be detected by looking at the discriminant of the polynomial in step 2 of my solution approach. For the special case of $x_0=y_0=c=0$, the relevant factor of the discriminant would be
$$
16a^4r^4
+ (- a^2b^4 - 20a^2b^2 + 8a^2)r^2
+ (b^6 + 3b^4 + 3b^2 + 1)
$$
As you can see, this is a quadratic polynomial in $r^2$. If both of its roots are positive, then all three cases can occur. You'd get two points of intersection if the actual radius is smaller than the smaler of these solutions, or larger than the larger one.
The special case is general enough
The special case of $x_0=y_0=c=0$ isn't that special after all. Simply substitute $x'=x-x_0$ and $y'=y-y_0$ into both your equations, and you get $x'^2+y'^2=r^2$ for the circle and the parabola will become:
\begin{align*}
a(x'+x_0)^2+b(x'+x_0)+c&=(y'+y_0) \\
ax'^2 +(2ax_0+b)x'+\underbrace{(ax_0^2+bx_0+c-y_0)}_{=0}&=y'
\end{align*}
So you can imagine $a'=a, b'=2ax_0+b, c'=0$ as the parameters of your translated parabola, and thus reduce the general case to this special case.
