Burgers' Equation Shock Solutions

Question

So what I'm confused about is how you go about finding shock waves. So suppose we are given the Cauchy problem for Burgers' equation $u_t + uu_x = 0$ with $u(x, 0) = 1$ for $x \le 0$ and $u(x, 0) = 0$ for $x> 0$. Then using method of characteristics we get $x = x_0 + t$ for $x \le 0$ and $x = x_0$ for $x > 0$. How do we then proceed, given that the characteristic lines will intersect so there is no unique $x_0$ such that $(x, t)$ are on only one characteristic line?

Answer 1

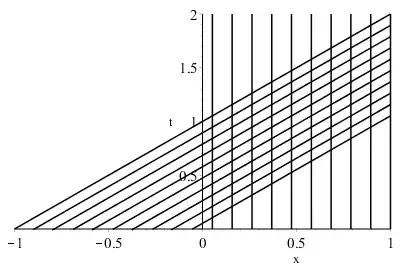
Here is a sketch of the characteristic curves in the $x$-$t$ plane, which equation is given by $$ \begin{aligned} x'(t) &= u(x(t),t) \\ &= u(x(0),0) \end{aligned} $$ Those curves intersect already at time zero:

Thus, a shock wave arises.

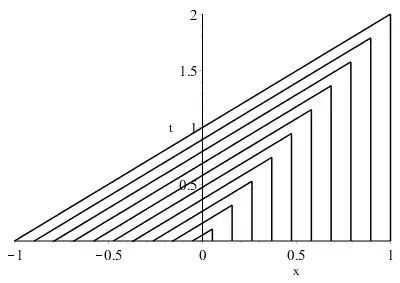
The Burgers' equation is rewritten in the conservative form $u_t + f(u)_x = 0$, where $f(u) = \frac{1}{2}u^2$. The shock wave with speed $s$, left state $u_L = 1$ and right state $u_R = 0$ writes $$ u(x,t) = \left\lbrace \begin{aligned} &1 &&\text{if}\quad x<st \\ &0 &&\text{if}\quad st<x \, . \end{aligned} \right. $$ The speed of shock must satisfy the Rankine-Hugoniot condition $s = \frac{f(u_R) - f(u_L)}{u_R - u_L}$, i.e. $s = \frac{1}{2}$. Here is a modified sketch of the $x$-$t$ plane, which accounts for the shock:

Answer 2

Follow the method in http://en.wikipedia.org/wiki/Method_of_characteristics#Example:

$\dfrac{dt}{ds}=1$ , letting $t(0)=0$ , we have $t=s$

$\dfrac{du}{ds}=0$ , letting $u(0)=u_0$ , we have $u=u_0$

$\dfrac{dx}{ds}=u=u_0$ , letting $x(0)=f(u_0)$ , we have $x=u_0s+f(u_0)=ut+f(u)$ , i.e. $u=F(x-ut)$

$u(x,0)=\begin{cases}1&\text{when}~x\leq0\\0&\text{when}~x>0\end{cases}$ :

$\therefore u=\begin{cases}1&\text{when}~x-ut\leq0\\0&\text{when}~x-ut>0\end{cases}=\begin{cases}1&\text{when}~x-t\leq0\\0&\text{when}~x>0\end{cases}=\begin{cases}1&\text{when}~x\leq t\\0&\text{when}~x>0\end{cases}$

Hence $u(x,t)=\begin{cases}1&\text{when}~x\leq t\\0&\text{when}~x>0\\c&\text{otherwise}\end{cases}$